Electrostatics and Electromagetism

Charge and Its Movements

Electrostatics and Electromagnetism

This page explains concepts at college level in the field of charged particles, storage (capacitors), motion of charged particles in electric and magnetic field, electro-magentic induction and electrical circuits.

Under construction

We appreciate your patient and you might be aware that it takes lot of effort to create a reliable, error-free content original content. In the mean time, please visit
this web page to get benefited by the excellent content provided by the website owner..

Basic Formula and Equations of Electrostatics

Force between charges placed in medium with absolute permittivity ε:

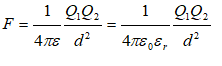
Force between charged particles

Here,
ε = absolute permittivity of the medium containing the charges particle
ε₀ = absolute permittivity of vacuum
ε_r = relative permittivity of the medium [= 1 for vacuum].

Electric Field or Intensity of Electric Field: This is force per unit area defined as E = F / q. Thus electric field due to a point charge Q at distance x from it is given by:
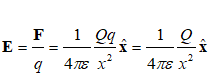
Electric Field - Point Charge

Here onwards, all the calculations are based on charges place in vacuum. The results are valid for any other medium where ε₀ is replaced by ε.

> Electric field due to ring of radius R with charge Q at distance x from the centre of the ring and perpendicular to the plane of the ring:
Electric Field - Circular Ring

Electric field due to circular disk of radius R with surface charge density σ at distance x from the centre of the disk and perpendicular to the plane of the ring:

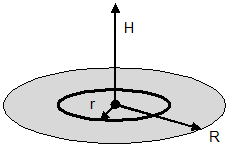
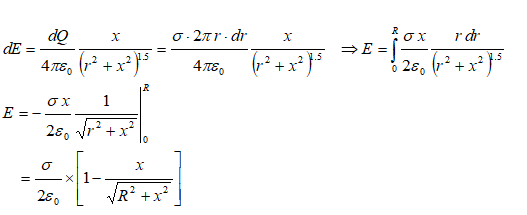
Electric Field - Circular Disk

It is assumed that the charge is only on one side of the plate. The results of electrical field due to thin circular ring described above can be used to derive the field as follows:

Electric Field - Circular Disk

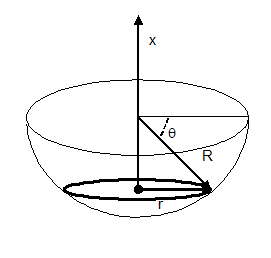
Electric field due to hemispherical shell of radius R with surface charge density σ at distance x from the centre of the sphere and perpendicular to the plane of the base:

Electric Field - Hemi-spherical shell

It is assumed that the charge is only on one side of the shell. The results of electrical field due to thin circular ring described above can be used to derive the field as follows, by replacing x by x+Rsinθ and r by Rcosθ:

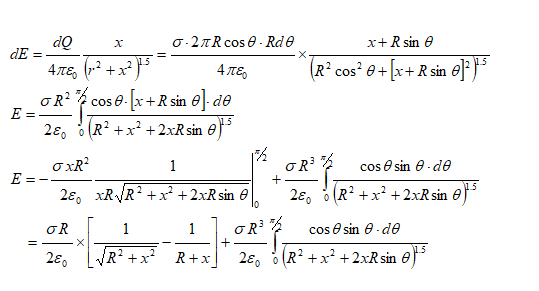
Electric Field - Hemishperical shell

The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.

Template by OS Templates