- CFD, Fluid Flow, FEA, Heat/Mass Transfer
Fluid Mechanics, Heat & Mass Transfer
Textbook Solutions: Fluid Mechanics, Heat & Mass Transfer, Aerodynamics
FM, HTX, MTX, AERO, COMBUSTION
This page is being continuously updated with complex (text-book type) problems in Fluid Mechanics, Heat Transfer, Aerodynamics, Mass Transfer, Combustion and Thermodynamics. The solutions to compressible flows including sub-sonic, sonic and supersonic flows inside a converging-diverging nozzle will be presented.
Table of Contents:
Buoyancy \-\ Plug Flow between Parallel Plates \-\ Flow through Pipe Branches forming Tee or Wye Network \-\ Equation of State: Soave-Redlick-Kwong Equation \-\ Half Filled Rotating TubeSummary of Hydrostatics
- For a plane surface immersed in a liquid in any orientation, the total normal pressure over the surface is P = A * ρ * g * h where h is the vertical depth of the centre of the gravity of the surface from free surface of the liquid, A is area of the surface.
- A plane surface immersed in a liquid is acted upon by a system of parallel forces which can be reduced to act on a single point of the surface known as centre of pressure.
- A curved surface immersed in a liquid is not acted upon a "system of parallel forces" and hence in general they cannot be reduced to a single force.
Centre of pressure of vertical rectangular plate
This is a very useful case which has frequent engineering applications.
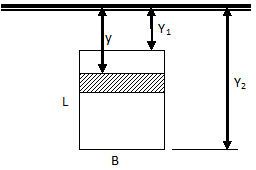

Similarly, for a triangular plate with base horizontal and at depth of Y2 and vertex up at depth of Y1, the centre of pressure is given by:
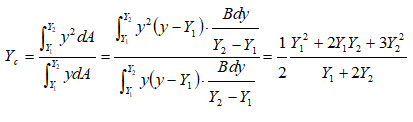
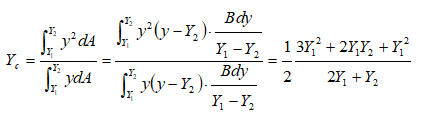
Centre of pressure of vertical circular plate
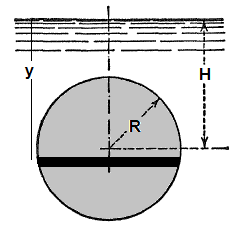
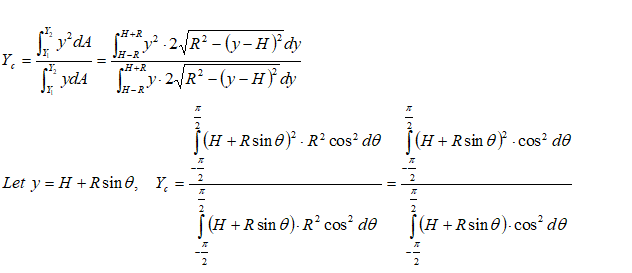
Even though the complicated definite integration is possible analytically, this is the time the introduce a simple method based on properties of sections. Note that the numerator of expression for centre of pressure is the "Second Moment of Inertia" or simply the Moment of Inertia about a "chosen axis" - typically the free surface of the liquid. The denominator is the "Moment of Area" about the same axis as chosen above - also known as "Statical Moment". Thus:
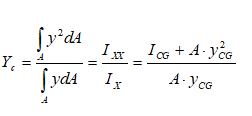
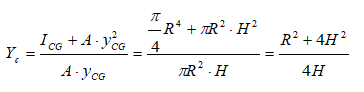
- If the area has axis of symmetry about the vertical axis, the centre of pressure will fall on it.
- Conversely, the centre of pressure will fall on the medial line, the vertical axis passing through the centre of gravity on the horizontal axis.
- The position of the centre of pressure is always below the centre of gravity of a surface.
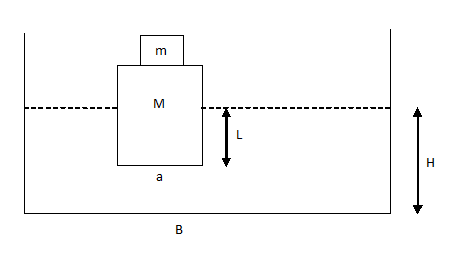
Buoyancy - Example Problem
A metallic block is floating along with a wooden block as shown in the figure below. If this metallic block falls into the tank, calculate the new depth of floatation and height of water level in the tank.
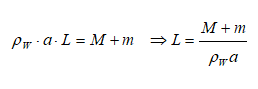
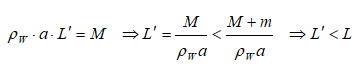
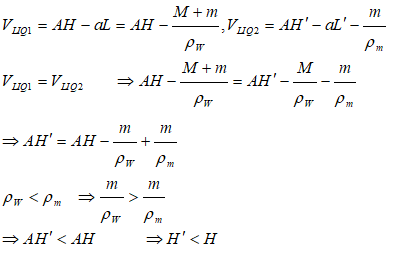
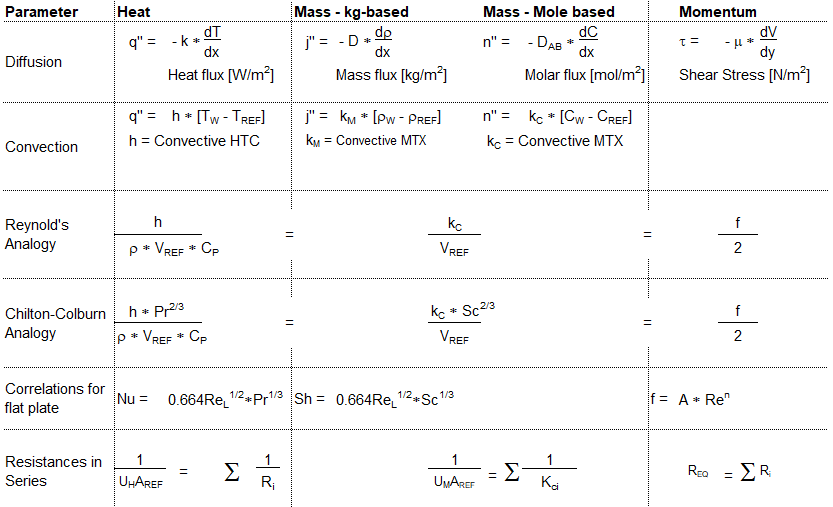
Analogy Between Fluid Flow, HTX and MTX
The method of relating two phenomena with some come feature is a powerful tool to both understand and remember the concepts. Following table summarizes key parameters which are analogous in the field of fluid flow (momentum transfer), heat transfer and mass transfer.
1D Heat Transfer with Convective Boundaries and Heat Generation
The designs of heat exchangers are the most predominant application of conductive heat transfer with such boundary conditions. The temperature profile in walls of a water-cooled internal combustion engine is also subject to this combination of boundary conditions though heat generation is not present in this application. Some applications can be current carrying conductor cooled by convection on both inner and outer diameters, nuclear fission in a annular cross-section cooled by convection on both the inner and outer radii. The governing equation and general solution of the differential equation is given by
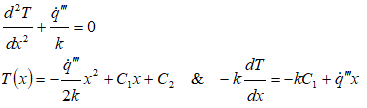
Heat flow is assumed positive from left to right. Hence, the convective heat transfer on left face is negative if ambient temperature is < wall temperature on the left face!
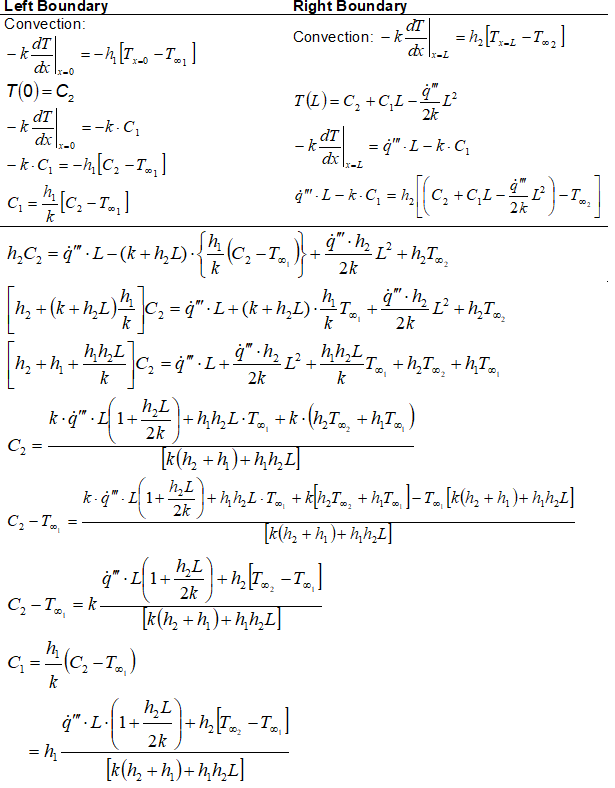
Finally, the temperature distribution function is expressed as:
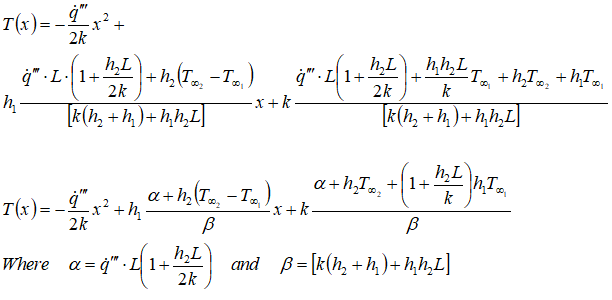
Plug Flow between Parallel Plates

Flow in an Annular Passage


Flow through Pipe Branches forming Tee or Wye Network
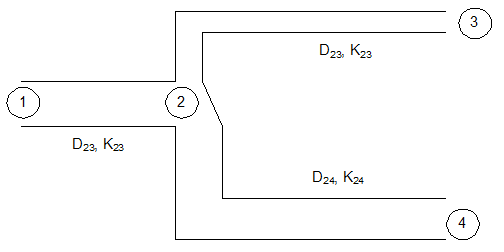
Note velocities in pipe branches 1-2, 2-3 and 3-4 are not known in advance and hence the loss coefficients KMN cannot be adjusted to same velocity. Note that the junction losses at node 2 can be incorporated either in K12 or in K23 and K24. It is more convenient to club the node loss in K12 as appropriate assignment into K23 and K24 will involve extra calculations.
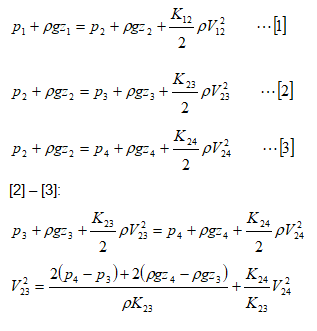
Denoting the pressures in terms of head of water column:
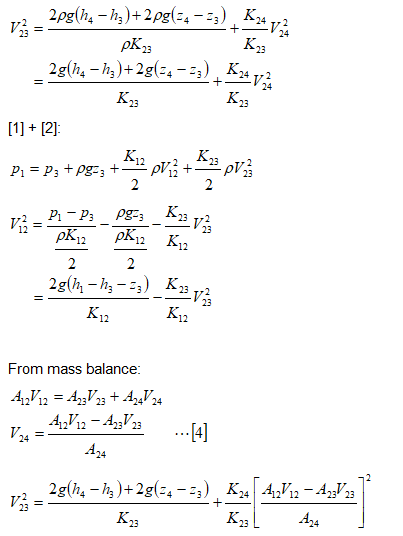
Simplifying further:
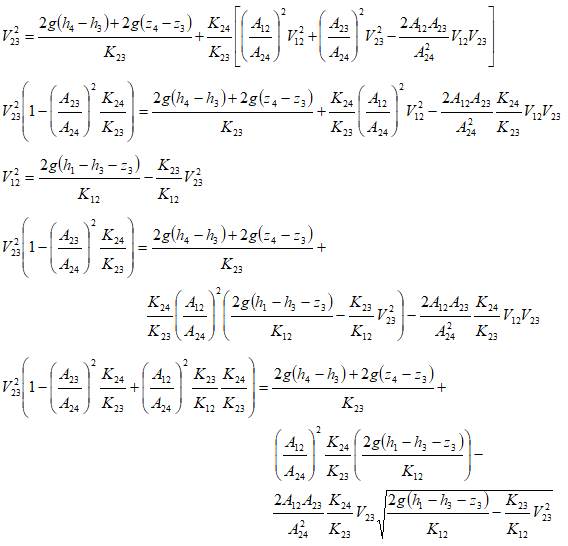
This is a non-linear equation in V23 and needs to be solved using trial-and-error or iterative approaches. Microsoft Excel Goal Seek utility can be used to solve this equation as well. A good initial guess would be required.
A more compact approach in terms of fluid resistances can be used as demonstrated below.

Thus, we have 3 equations and 3 unknowns – but they are still non-linear and needs to be solved using iterative method.
Force on a curved pipe with varying cross-section
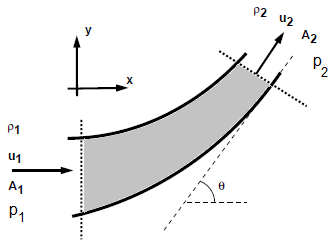
A reducing bend having diameters D upstream and d downstream, has water flowing through it at the rate of m [kg/s] under a pressure of p1 bar. Neglecting any loss is head for friction calculate, the horizontal and vertical components of force exerted by the water on the bend.
Newton's Law of Motion applied to Fluid Elements:
F = m [u2 - u1]Newton's Third Law Applied to Pipe:
This is the force acting on the fluid and only means to apply the force on the fluid is the walls of the pipe. Hence, from Newton’s third law, and equation and opposite force will act on the pipe.
ΔΓX = m * [u2X - u1X] = FΓX. Thus: FΓX = m * [u2 cos(θ) - u1]ΔΓY = m * [u2Y - u1Y] = FΓY. Hence, FΓY = m * [u2 sin(θ) - 0] = m * u2 sin(θ)
Force on fluid element due to pressure at boundaries
FpX = p1A1 - p2A2cos(θ)FpY = 0 - p2A2sin(θ)
Use Bernoulli’s equation to find p2 in terms of other known parameters:
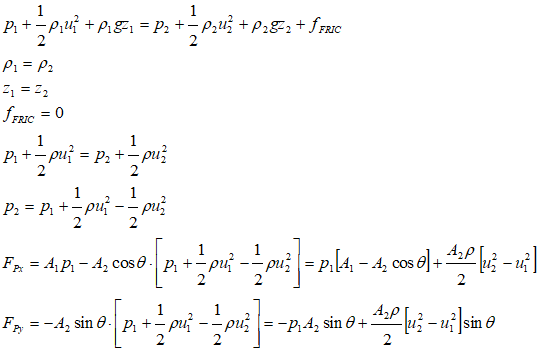
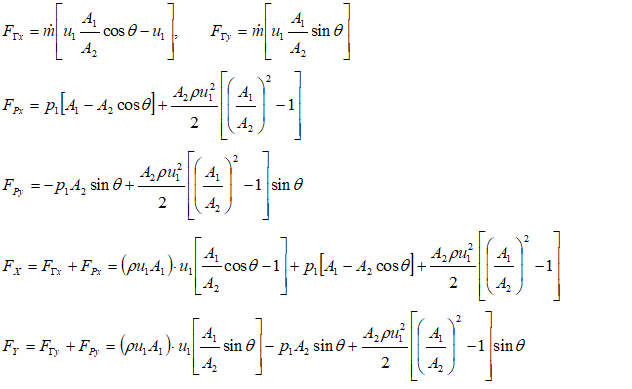

If pipe is straight
θ = 0 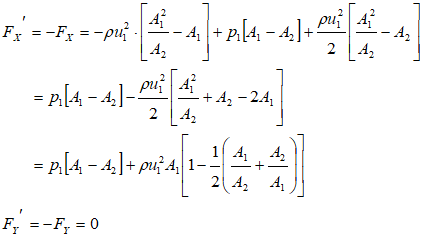
Equation of State: Soave-Redlick-Kwong Equation
or gases at very high pressure and those in liquid state such as Liquified Petrolium Gas (LPG), the accuracy of ideal gas equation falls sharply. Many improvizations have been made and SRK equation is one such method. The approach is demonstrated using following sample problem:
A gas cylinder with a volume of 5.0 m3 contains 44 kg of carbon dioxide at T = 273 K. estimate the gas pressure in [atm] using the SRK equation of state. Critical properties of CO2 and Pitzer acentric factor are: Tc = 304.2 K, pc = 72.9 atm, and ω = 0.225.
General cubic equation of state is given by following equation
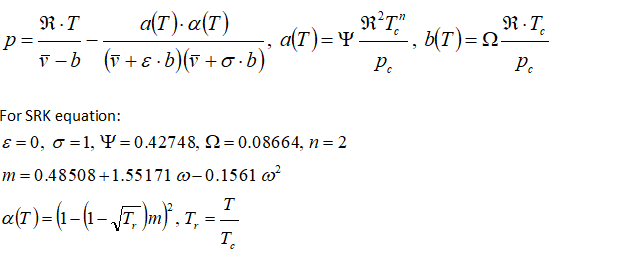

Alternatively, the equation can be solved using Newton's method as described below.
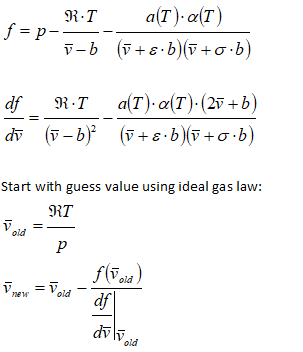
Half Filled Rotating Tube: A circular tube is half full of liquid and is made to revolve around a vertical tangent line with angular velocity ω. If radius of the tube is R, calculate the angle between horizontal and diameter passing through the free surface of the liquid.

The tube is rotating about red line and the liquid level is shown by yellow zone. Point 'D' is the lower most point of free surface, θ is the angle which needs to be calculated.
The pressure at any location is given by: dp = ρ (ω2r.dr + gdz) where r is the distance of the point from the axis of rotation and z is the distance of the point from the origin. The point 'D' is rotating at radius r = R(1-cosθ), z = R.sinθ and is at p = 0. Another known point 'C' is at pressure zero, r = R(1+cosθ), z = -Rsinθ. Note that +z is along the downward direction (this is only a convention).


Liquid filled in rotating conical pot: A conical pot of height H and vertical (full cone) angle θ contains liquid k-times (x < 1) the volume of full cone. Find out the minimum angular velocity at which shall prevent liquid overflowing the cone.

Thus; z = (1-k).2H/3 ... [1] Also, from paraboloid of revolution (latus rectum): 2g/ω2 = R2/z ⇒ z = ω2.R2/2/g ... [2]
To prevent overflow: z ≤ (1-k).2H/3From equations [1] and [2], ω2.R2/2/g ≤ (1-k).2H/3 ⇒ ω ≤ [4g/3.(1-k).H/R2]1/2
R = H . tan(α) ⇒ ω ≤ [4g/3H.(1-k)]1/2.cot(α), thus if k = 0.5, ω ≤ [2g/3H]1/2.cot(α)A closed circular cylinder is just filled with water and rotates about a vertical. Find the ratio of total thrust on the bottom to that on the top when the angular velocity is ω, H is the height and R the radius of the cylinder.
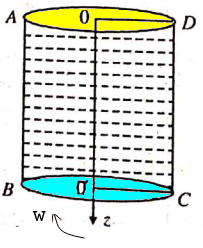
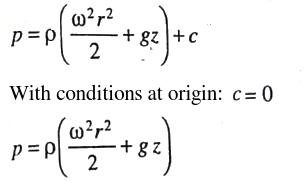

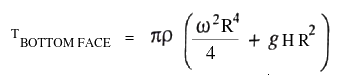
Fluid Pressure in Rotating Reference Frame
Bernoulli’s equation in the rotating frame where rotation is around z-axis: p(r, z) + ρgz + V(r) = p(r, z) + ρgz − ρω2r2. For a container open to atmosphere, gauge pressure at all points on the interface is zero i.e. p(r, z) = 0. Elevation of the free surface to the radial location: z = ω2r2/2/g.For a container rotating cylindrical about its axis: the shape of the free surface is a parabola and fluid inside the rotating cylinder forms a paraboloid of revolution, whose volume is one-half of the volume of the "circumscribing cylinder". To calculate angular velocity at which the liquid at the center reaches the bottom of the cylinder just as the liquid at the curved wall reaches the top of the cylinder: ωspill = (2gH)0.5/R.
Ball in rotating tube
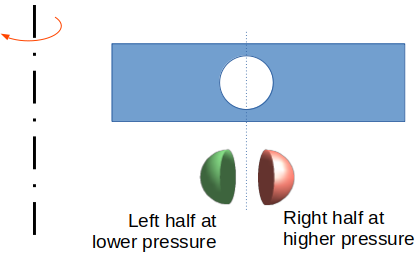
The centroid of a hemi-sphere is at 3R/8 from the base. Using this value, pressure on the left half of the ball = 1/2.ρF ω2(r-3R/8)2. The pressure on the right half of the ball = 1/2.ρF ω2(r+3R/8)2. Net force acting on the ball towards the axis of rotation = 1/2.ρF ω2(4.r.3R/8)2 × π*R2 where projected area = π*R2.
Net force due to fluid pressure towards axis of rotation, FF = 1/2.πR2.ρF ω2(r.3R/2) = 3/4πR3.ρF ω2r
Centrifugal force due to own mass of the ball, FB = 4/3.πR3.ρB ω2r
The position of the ball can be estimated using inequality FB ≤ FF. Will the ball get pushed towards inner radius for all densities of the ball? This method yeilded incorrect conclusion as the pressure on the surface of spherical ball was assumed to be varying linearly with radius instead of parabolic variation as per formula p(r) = p(r = r0) + 1/2.ρFω2r2. The correct derivation of net fluid forces acting on the ball are given below: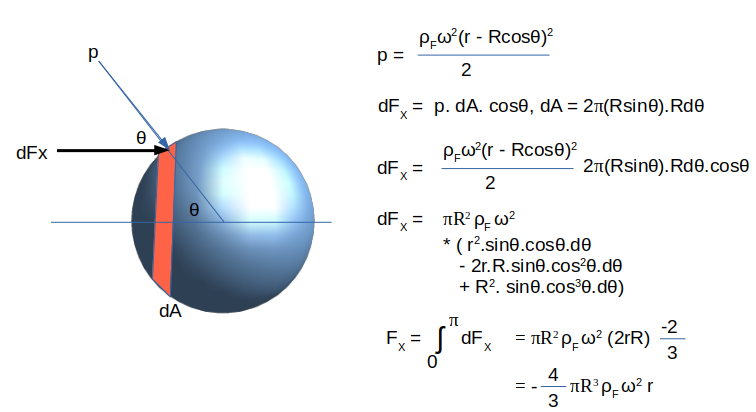
The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.
Template by OS Templates