Extended Surfaces and Heat Spreaders

Octave Script

Heat Transfer in Straight Fins

Fins as extended surfaces have wide applications in heat transfer augmentation techniques. The solutions are already available in analytical form. This OCTAVE script tries to prepare a plug-and-calculate method for straight fins for all possible combinations of boundary conditions.

Temperature Plots

Note that the heat transfer at base is 9.867 [W]. This value can be used to calculate temperature profile T(x) for "Heat Flux" (base) - Adiabatic (tip) boundaries to ensure that the temperature at base is same as in previous case. This is sort of the quality assurance (QA) method for the code and not the analytical methods described in the textbooks on heat transfer.


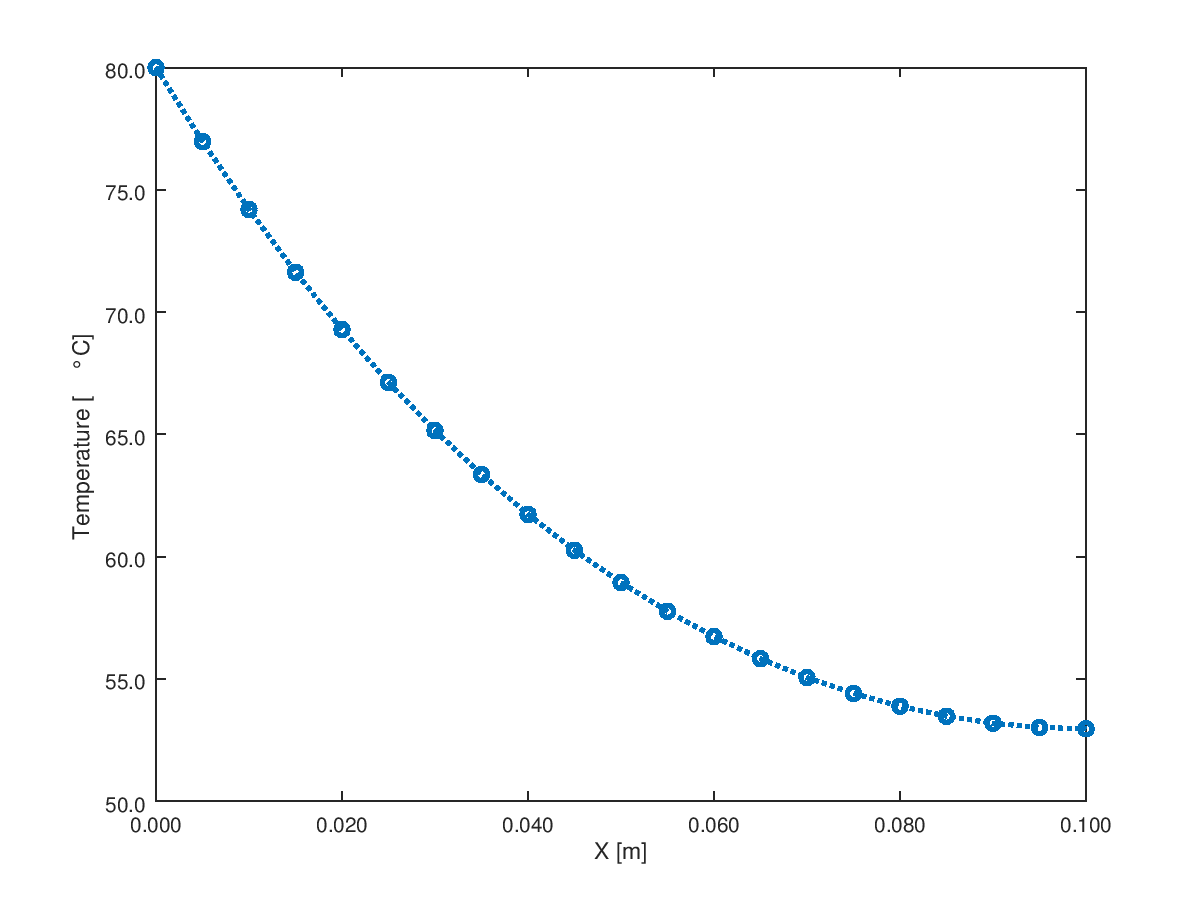
The effect of convection from tip is insignificant where the convective heat transfer has been assumed to be same as on the primary surface of the fins. The heat loss from base of the fin increased only to 9.948 [W]


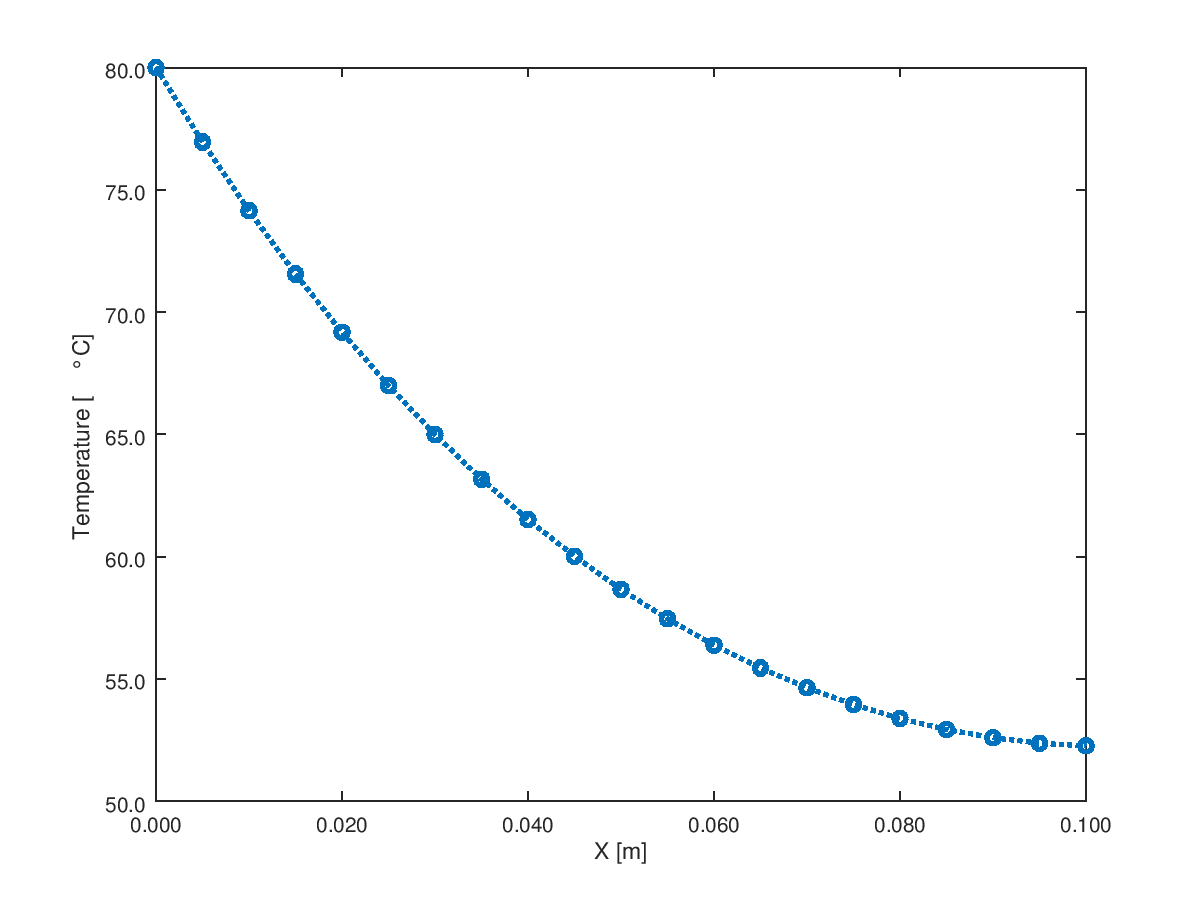
Other boundary conditions can be used to iterate the designs to meet specific requirement such as temperature at the tip, temperature gradient .... The complete script is as follows.

% Fin performance calculation for all possible boundary conditions
% 
  clear; clc;
% Thermal conductivity of fin material in [W/m.K]
  k = 200;
%
% Convective heat transfer coefficient over fin surface in [W/m^2.K]
  h = 100;
  TREF = 30; 
%
% Perimeter of the fin [m]
  p = pi*0.01;
%
% Cross-section area of the fin [m^2]
  A = pi/4*0.01^2;
%
% Length of the fin in [m]
  L = 0.10;
%  
% Boundary condition at base: 1 - Known temperature [C] - T0 
%                             2 - Heat flux [W/m^2] - Q0
%
  BC1      = 1;
  valueBC1 = 80; %9.8675/A;
%
% Boundary condition at Tip: 1 - Known temperature [K], 
%                            2 - Known heat flux [W/m^2] (< 0 if heat loss)
%                            3 - Convection, h_tip = h [W/m^2-K], TREF2 = TREF
% Note that "positive value" of heat flux is heat flow into the fin body.
  BC2      = 3;
  valueBC2 = h;   % TL or QL or hTip 
  
%
% Number of calculation points [recommended to be an odd integer]
  n = 21;         

% -------------User Input Ends ------------------------------------------------
%---------------------+------------------+------------------+------------------  

  x = [0 : L/(n-1): L];
  m = sqrt(h * p / k / A);
  b = sqrt(h * p * k * A);
  T = zeros(n);
  if (BC1 == 1)
    if (BC2 == 1)
	   Tr = (valueBC2 - TREF) / (valueBC1 - TREF);
       Tx  = TREF + (valueBC1 - TREF) .*  (sinh(m .*(L - x)) ./ sinh(m .* L) ...
	               +  Tr .* sinh(m .* x) ./ sinh(m .*L));
       Q0 = b * (valueBC1 - TREF) * (1 / tanh(m * L) - Tr / sinh(m * L))
       QL = -b * (valueBC1 - TREF) * (1 / sinh(m * L) - Tr / tanh(m * L))
 	   T0 = valueBC1
	   TL = valueBC2
%
    elseif (BC2 == 2)
	   qL = valueBC2 / k / m;
	   q0 = valueBC1 - TREF;
       Tx = TREF - (qL + q0 .* sinh(m .* L)) ./ cosh(m .* L) .* sinh(m .* x) ...
	             +  q0 .*  cosh(m .* x);	
       Q0 = b * (qL + q0 * sinh(m * L)) / cosh(m * L)
	   QL = valueBC2 * A
	   T0 = valueBC1
	   TL = Tx(end)
%	   
    elseif (BC2 == 3)
	   hr = valueBC2 / k / m;
       Tx =  TREF + (valueBC1 - TREF) .* (cosh(m .* x) - (hr + tanh(m .* L)) ...
	            ./ (1 + hr .* tanh(m .* L)) .* sinh(m .* x)); 	
       Q0 = b * (valueBC1 - TREF) * (hr + tanh(m * L))/ (1 + hr * tanh(m * L))
	   QL = -valueBC2 * A * (Tx(end) - TREF)
	   T0 = valueBC1
	   TL = Tx(end)
	end
  end
%  
  if (BC1 == 2)
    if (BC2 == 1)
	   Qr = valueBC1 / k / m;
	   Tx = TREF - Qr .*  (sinh(m .* x)) + ((valueBC2 - TREF)+ Qr .*  ...
	               sinh(m .* L)) .* cosh(m .* x) ./ cosh(m .* L);
       Q0 = valueBC1 * A
       QL = -b * (Qr * cosh( m * L) - ((valueBC2 - TREF) + Qr * ...
	             sinh(m * L)) * tanh(m * L))
	   T0 = Tx(1)
	   TL = valueBC2
%	   
    elseif (BC2 == 2)
	   Qr = valueBC2 / valueBC1;
       Tx = TREF + (valueBC1 .* A ./ b) .*  (cosh(m .* (L - x)) ...
	             ./ sinh(m .* L) + Qr ./ tanh(m * L));	
       Q0 = A * valueBC1
	   QL = A * valueBC2
	   T0 = Tx(1)
	   TL = Tx(end)
%	   
	elseif (BC2 == 3)
	   hr = valueBC2 / k / m;
	   qT = valueBC1 / k / m;
       Tx = TREF - qT .* sinh(m .* x) + qT .* (1 + hr .* tanh(m .* L)) ...
	            ./ (hr + tanh(m .* L)) .* cosh(m .* x);
	   Q0 = valueBC1 * A		
       QL = -valueBC2 * A * (Tx(end) - TREF)
	   T0 = Tx(1)
	   TL = Tx(end)
	end
%	
  end 
% Plot temperature profile
  plot(x, Tx, "linestyle", ":", "linewidth", 2, "marker", "o");
  xlabel('X [m]'); ylabel('Temperature [\degC]');
%  
  % Format X-axis ticks
  xtick = get (gca, "xtick"); 
  xticklabel = strsplit (sprintf ("%.3f\n", xtick), "\n", true);
  set (gca, "xticklabel", xticklabel)   
%  
  % Format Y-Axis ticks
  ytick = get (gca, "ytick"); 
  yticklabel = strsplit (sprintf ("%.1f\n", ytick), "\n", true); 
  set (gca, "yticklabel", yticklabel);
%
  print -dpng finTempAdiab.png -color -landscape;
return