- CFD, Fluid Flow, FEA, Heat/Mass Transfer
Computational Domain
Solution Domain
Geometry or computational domain for CFD simulation requires a water tight geometry with simplification to handle the mesh creation process. Solution of computational domain refers to 2D or 3D geometry in which fluid flow and/or heat transfer phenomena need to be solved. This is known as "ZONES" in FLUENT, "REGIONS" in STAR-CCM+ and "DOMAIN" in CFX. These are "volumes surrounded by closed surfaces(called boundaries)" in 3D and "areas closed by edges or lines (called boundaries)" in 2D. It is the mesh and nodes generated to define and represent the physical space mathematically. No geometrical information is associated with the solution domain.
Geometry Clean-up Steps [+] Dimensional Values to be Recorded {*} Defeaturing in ANSYS Discovery |:| Values to record about computational domain [+] Blender for Geometry Clean-up |+| Create Periodic Planes |:| Domain size reduction by sub-modeling ]=[ CAD Data Exchange [=] Parametric Geometry Creation [*] Recommendations for Parametric Modeling [=] Create Driving Dimension using Measurements from within the Pull Tool ]*[ Objects, Selections and Named Selections |=| Setting Colour of Faces |+| Power Selection {*} Creating cylinders by extruding surfaces }={ External Connections (:) Remove all chamfers and rounds |\/| Basic Operations: Open - Save - Import |/\| Remove - Translate - Copy Holes \:/ Create Fluid Volume [?] Get and Set Dimension Values
Scripting in ANSYS Discovery [*] Script to move objects defined by Named Selections \*/ Scripting in ANSYS DesignModeler
The geometry creation for CFD can be accomplished by either of the following two methods:
- Create geometry in any CAD (Computer-Aided Design) software such as Unigraphics, Catia, Pro/E, Solidedge. The geometry information created so far is called to be in "Native CAD" format. This geometry should be translated to a Neutral format such as IGES, STEP, Parasolid. All Pre-processors available has build-in capacity to read (Import) CAD data in this format. Once the geometry is imported into the Pre-processor, defeature as per requirement.
- The second approach is to create geometry directly into the pre-processor. All commercial pre-processors has basic built-in features to create Geometrical Entities. We strongly recommend this approach for following two cases:
- 2D simulation
- When geometry is axisymmetric. In this case, one needs to create the 2D cross-section first and then extrude it by rotation. In ANSYS FLUENT, in the axisymmetric model the boundary conditions should be such that the centerline (where the radius reduces to zero) is an axis type instead of a symmetry type. The axis should the z-axis. Thus, for all 2D simulations, FLUENT expects geometry to be in XY-plane.
- One widely used term in numerical simulation is Topology. A precise explanation is provided by Georgios Balafas in his master's thesis for the Master of Science program in Computational Mechanics "Polyhedral Mesh Generation for CFD-Analysis of Complex Structures": The topology of a mesh is an abstraction of the geometric model, that provides unambiguous, shape independent information about the relation between the entities that form the mesh structure. To this end, a mesh database is used in order to store various-level attributes of entities of different dimensions. These typically include 0-D entities, referred to, in literature, as vertices or nodes, 1-D entities, referred to as edges, 2-D entities, referred to as faces or facets and 3-D entities, referred to as solids, volumes, regions or cells.
- Few other definition taken from previous reference:
- "A face is said to be classified on the boundary of the geometric model, when it is adjacent to only one solid, which means that the free side of the face forms an external boundary. In the opposite case, where a face is adjacent to two solids, it is classified in the interior of the geometric model."
- Mesh edges inherit their classification by their adjacent faces. Specifically, when an edge has at least one adjacent face that is classified on a model's boundary surface, the edge is also classified on the same boundary. To be more precise, in a conforming non-manifold three-dimensional mesh, an edge will have either zero or at least 2 adjacent boundary faces, however detecting one of them can be considered enough to classify the edge on the boundary as well. Furthermore, when an edge's adjacent boundary faces are classified on different boundary surfaces of the model, this denotes the edge's classification on a model's boundary edge, where 2 of its boundary surfaces intersect.
- It is, therefore, adequate to count the amount of different boundary identifiers that are assigned to the adjacent faces of an edge, in order to conclude whether this edge is internal (zero boundary identifiers), on a boundary surface (one identifier), on a boundary edge (2 identifiers), or is a non-manifold edge (> 2 identifiers).
- Extending the aforementioned classification criteria for vertices, a mesh vertex is classified on a model's boundary surface, when at least one of its adjacent edges is also classified on a boundary surface. Additionally, when at least one of the adjacent edges of a vertex is classified on a model's boundary edge, then the vertex is also classified on the same boundary edge. Finally, when there exist at least two adjacent edges classified on two different model's boundary edges, the vertex is classified on a model's corner, formed at the intersection of the boundary edges. In other words, the classification of a vertex with respect to the model can be determined by counting the amount of different boundary identifiers assigned to the adjacent faces of the vertex.
- Zero boundary identifiers denote an internal vertex, while vertices on a boundary surface have adjacent faces with a unique identifier. Nodes on model's boundary edges have adjacency relationships to faces of two boundary identifiers in total and vertices on a model's corner sum up with three adjacent boundary identifiers. Finally, when a vertex has adjacent faces classified to more than three different boundary surfaces, the vertex is non-manifold.
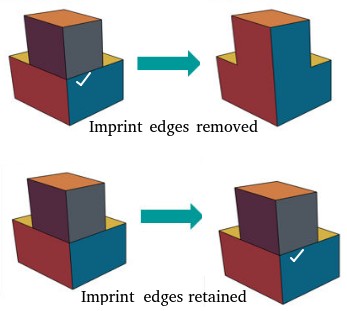
Other operations include: extract centrelines (to plot variation of pressure or temperature vs. position), create mid-planes (to create plots on a non-planar surface), save curve data into .csv file, create enclosure, merges faces, create body-of-influence (BOI) geometry, create Face of Influence (FOI) geometry, scale-up or down a body... ANSYS Discovery has option to create Curve Tables and Hole Tables (Curve Table in the Annotation group under Detail tab), the centreline of a tube can be generated using 'Extract' tool in Beam section under Prepare tab. Fill Surface: create surfaces from free edges of a hole in a facet sheet body, Sew Sheet bodies: combine or sew multiple facet bodies into a single body, Bridge surface: (similar to loft operation in some CAD tools) create a body between two sets of edges of existing facet bodies. Extruding surfaces and sketches directly up to any user defined Plane with the "Up to Plane" method. Keep or delete imprinted edges when uniting bodies.
Creation of post-processing planes: when computational domain is not aligned to coordinate axes or the flow path are curved and twisted that any section would result in multiple non-contiguous surfaces, it is strongly recommended to create post-processing planes during geometry creation and meshing process. These faces should be named with prefix 'post_' and set as internal type in meshing (so that boundary layers do not grow over them). Though most of the solvers and post-processors has option to import such surfaces in STL format and imprint on the mesh, it is time consuming and may result in interpolation error. The 'internal' zone created shall have faces and nodes aligned on it and the solution variables are directly available there to calculate derived parameters such as mass flow rate and pressure. In case of imprinted surfaces, the solution variables have to be interpolated from nearest nodes, face and cell centers.
Unit Systems
Every designer needs to work on length units and thus all CAD modeling program or tool have some built-in features for default units and ways to convert from one units to others. The following image describes options to select unit system in SCDM.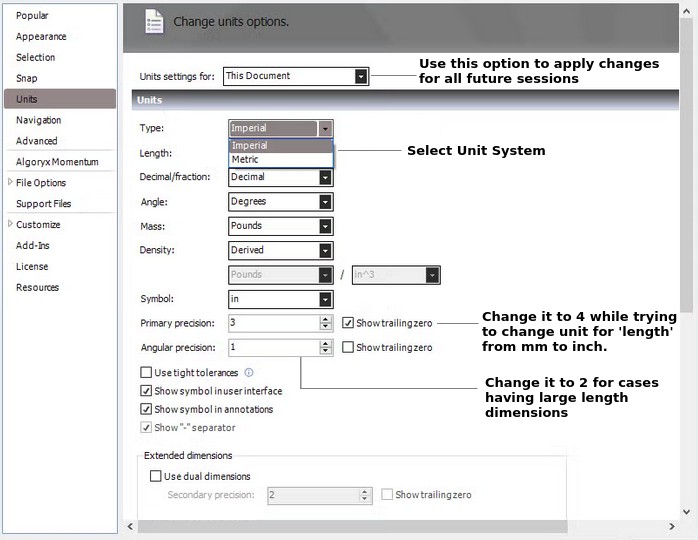
All tools dealign with virtual geometry and mesh generation has option to scale the model. As units are not mentioned at every numerical value, scaling changes the value as per units specified. For example, for a cylinder the tool may contain information 'mm' in header row and only numbers for diameter, length and other key points (nodes, vertices...). When user changes the units to 'm', those values has to be divided by 1000 while only the header gets changed from 'mm' to 'm'.
Geometry Clean-up Steps
Pre-requisite: get familiar with the tool being used and do not rely on similar features in tools from same product family. ANSYS Discovery which is the successor of SpaceClaim, has many features under different user menu. For example, in ANSYS Discovery the colour of faces and bodies are set using icon in the model tree and not with (right click) context menu. The right click after selection of a body does not give option to set transparency. HUD: Head-Up Display is a new feature which may seem a nuisance to someone new to Discovery.
The first step is to know the geometry. If it comprise of sheet metal parts such as fan shroud, it requires handling thin bodies, sharp bends with gap, forming clearance... If the geometry consists of plastic parts, it will have fillets of variable radii and the two adjacent parts may not align properly. The plastic parts usually have lot of ribs and hidden cavities not visible from outside. One trick is to scan through section tool in all three direction and get the insight into the extent and complexity of defeaturing required. This may require 2 to 6 hours.The second step is to organize the geometry into sub-groups easy to handle in batches. This requires moving the bodies into components, renaming them to identify easily. The bodies needs to be grouped into solid, fluid and empty categories. This may take another 2 - 4 hours of effort. Refer to Naming Convention for basic idea.
The third step is deletion of unwanted parts: screws, clips, clamps, body inside another body... and filling cavities, gaps, converting thin sheets to zero-thickness walls or thickening them to get less skewed cells. (Note: If the faces are coloured within the CAD software, SpaceClaim recognizes those colours as "named selections" and transfers them to "Mesh" and "CFX-Pre"). This may take 1 to 2 days based on maturity of the input CAD geometry.The fourth step is to remove small blends (fillets), chamfer, proximities (tangential contact between two curved bodies or a curved face and a flat surface....), extra edges (edges at tangential splits) and combine or segregate bodies into logical groups. Note that removing fillets should always be the last step of defeaturing process. This step may take 4 hours to 2 days.
The fifth step is to save geometry into multiple files based on ease of meshing. Many a times it is better to generate surface mesh into multiple groups and assemble them later especially when there are thin sections. Sometimes it becomes a necessity to split geometry into extrudable volumes.
The sixth step is to create monitor plane(s) and name them appropriately such as int_mon_fan_up or int_mon_delta_p... This is helpful in case any section surface of the domain creates multiple non-contiguous regions. In ANSYS Fluent, either a clipping operation after surface creation is required or the monitor plane needs to be imported as STL mesh and imprinted in Pre-Post.
Thus, the clean-up activity may take 2 days to 4 days (this excludes mesh generation activity). Note that one may need to iterate between surface mesh and geometry clean-up especially to remove proximities and self-intersections (which may occur despite successful topology sharing). It requires 5 to 10 times more effort to address geometrical challenges inside meshing tool than the CAD tool.Notes:
In ANSYS SpaceClaim, do the Pull operation by isolating the body (that is hiding other bodies). By default, Pull operation shall try to merge all visible objects (and No merge option needs to be activated for every pull operation).To remove proximity between curved faces, pull the common edge to create a blend or chamfer. Sometimes, merging or collapsing of sliver faces in SpaceClaim is not feasible. These faces can be put into a separate Named Selection (Group) such as ns_sliver_faces utilizing Power Selection feature. Later the boundary elements on these faces can be collapsed in Fluent meshing.
It is better to unite (merge) two bodies than keep them separate (joined) by shared topology. However, this is possible only when the volume occupied by those bodies are empty (void). In case the two bodies cannot be combined (merged), delete the common surfaces (let them be surface bodies than solid bodies) - however such operations should be performed as last step before taking the data to pre-processor.Ansys SpaceClaim has a tool named Sharp Edges which highlights edges sharper than the Max edge angle (the angle between normals of faces that share an edge) specified. It has another tool 'Clearance' in the 'Detect' group of the 'Prepare' tab which might be helpful to find out why two bodies cannot be united when they seem to be touching each other.
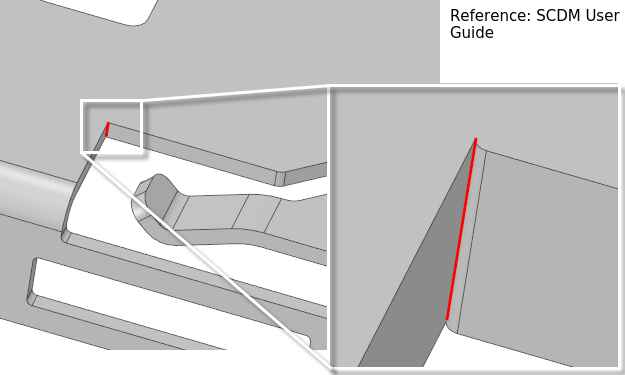
Refer to checklist for mesh generation and update geometry appropriately. Values to be recorded about computational domain - multiple values can be typed separated by comma. Note that it is better to start recording the information to be put in a report from the start rather than preparing the report at the end of the simulation activities.
| S. No. | Description of the Dimension | Value(s) |
| 01 | Orientation (such as direction of gravity) | |
| 02 | Rotation axis (or flow direction) of the fan | |
| 03 | Coordinates of a point on axis of the fan | |
| 04 | Total surface area | |
| 05 | Total volume | |
| 06 | Cross-section area of the inlet(s) | |
| 07 | Cross-section area of the outlet(s) | |
| 08 | Number of fluid-fluid interfaces and names | |
| 09 | Number of fluid-solid interfaces and names | |
| 10 | Number of solid-solid interfaces and names | |
| 11 | Fan hub, tip and shroud diameters | |
| 12 | Thickness and cross-section area of porous domain(s) | |
| 13 | Thickness of printed circuit board and normal direction | |
| 14 | Dimensions of heat sink: thickness, pitch, length, radius |
Parametric Modeling (Geometry Creation) within CFD Environment
For optimization studies, ANSYS Workbench offers options to make simulations in the order defined as DOE (Design of Experiment) table, each row termed as Design Point. ANSYS SpaceClaim and Discovery has option to parametrize the geometrical operations such as Pull, Move... which can be used to change the shape, size and location of bodies. Such activities are specially important in situations where periodicity and symmetry exist such as heat exchangers, fins, external aerodynamics.Parametric Modeling in ANSYS SpaceClaim / Discovery: For all operations which can be parametrized, the symbol 'P' in SpaceClaim and icon within context-menu in Discovery appear to create a parameter. The value field of a parameter can contain basic formula such as 0.02 * 25.4 to convert a dimension from inch to 'mm'.
The Groups tab contains Named Selections, Driving Dimensions and Script Parameters. Driving dimensions can be Measurement, Ruler Dimension, Pattern Count... When a Pull operation is initiated, the option to make it parametric appears only after a value is entered (after pressing the space bar). Similarly, Ruler Dimension can be used to change the size as shown below in one of videos from Ozen Engineering.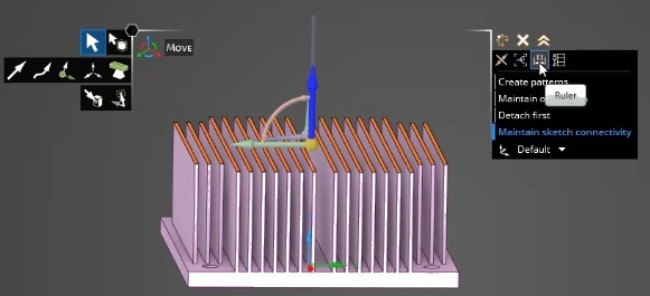
"Driving dimensions are created when there is a dimension on screen or a dimension in the properties panel." For example, selecting the round (fillet) and then clicking Create Group in the 'Groups' panel creates a "driving dimension" instead of a "named selection" because the face selected is a round, which has a dimension property that can be controlled from the property panel. Similarly, a "round group" is created each time fill operation is used to create a round (fillet) and is saved in the Filled Rounds folder.
Note: clicking on a driving dimension created with 'Pull' operation automatically activates the 'Pull' operation ↴
Note that the GUI in the two videos are a bit old and in recent versions, Create Group has been replaced with Create NS and Create Parameter. When a dimension is showing and "Create Parameter" is clicked, it usually create a driving dimension with initial value appearing on the screen. The orientation of Move handle can be changed by using the Direction tool guide, holding Alt and selecting a reference object, or by dragging a ball on the axes of the Move handle. That is, Alt + click a point or line orients one of the axes of Move handle towards that point or along that line. Alt+click on a plane, the direction of movement is set perpendicular to the plane. Steps to create Driving Dimensions using Move operation ↴The behaviour of the Move tool changes based on what is selected and direction of axes of move handle change based on the orientation on the screen. Press Ctrl to copy the object selected for movement and place it at the location at which user drags or dimensions the move. Video titled "Using ANSYS SpaceClaim and ANSYS Discovery for Parametric CAD Modeling" from KETIV Technologies gives good explanation of the methods described above. As per help.spaceclaim.com/2016.0.0/en/Content/Groups.htm: Group order is important because they are changed from top to bottom when the change is initiated in an external application.
Steps to create Move handle at 'Zero' initial value is explained below. The yellow centre sphere of Move handle turns into a blue cube when the Move handle is anchored.
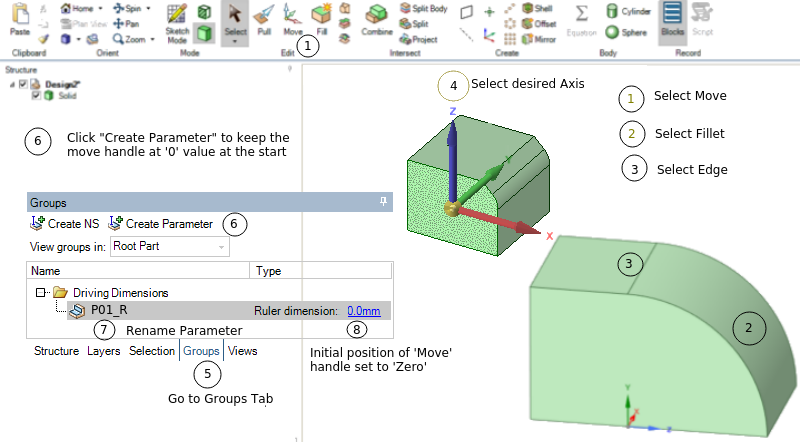
- Select face(s) or object(s) to be moved
- Press 'm' or click 'Move' icon under 'Edit' group in Ribbon bar
- Select anchor point or edge
- Select axis on the Move handle
- Press space bar on keyboard ('0' will appear near Move handle origin)
- Click 'Enter' key (to accept '0' as initial value)
- Click on "+Create Parameter" icon in Group tab to create the Driving Dimension.
Move operation is very much similar to Pull operation though the behaviour of the Move tool changes based on what is selected. Though Pull allows operation in only one direction, Move allows operation in multiple directions. If an entire object, such as a solid, surface, or sketch is selected, 'Move' operation translates or rotates the object. If one side of a solid, surface, or sketch is selected, move operation shall enlarge or reduce the size of the object. If an object is moved into another object in the same component, the smaller object is merged into the larger one and receives the larger object's properties. Moving the apex of a cone changes the height, Anchor the Move tool to the outer face to scale the cone.
By default the 'Move' handle seems to be placed at the centroid of chosen objects (faces, edges...). However, there are cases when an axis was create using same set of objects, the location of origin of the axis and location or the origin of move handle were not coincident. In absence of clear documentations, following error may occur.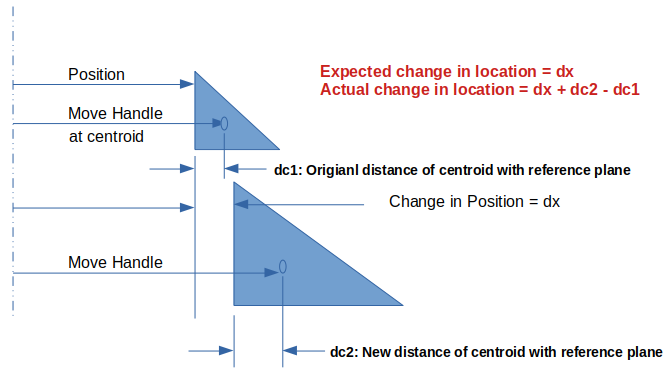

Create Driving Dimension using Measurements from within the Pull Tool: referenced from User Guide
- Enter the Pull tool and select an object(s) to pull
- Enter the Measure tool (shortcut is e) and measure any single object or measure between two objects
- Click the measurement result that will drive the Pull (hover over measurements output box to display a purple box)
- Once selected, that single measurement will display on screen with arrows pointing to either object chosen for measurement
- Click in the highlighted dimension box and open the Groups panel
- Click "+Create Parameter" and the measurement group gets created.
From Workbench (V20) User Guide: "Negative dimension values can invert the direction vector of operations with which they are associated. This change is applied to the current and subsequent design point updates. As a result, when a Workbench input parameter is used as a driving dimension for a geometry, negative dimension values can result in unexpected geometric changes."
Geometry Fully or Partially Enclosed in a Fluid Domain
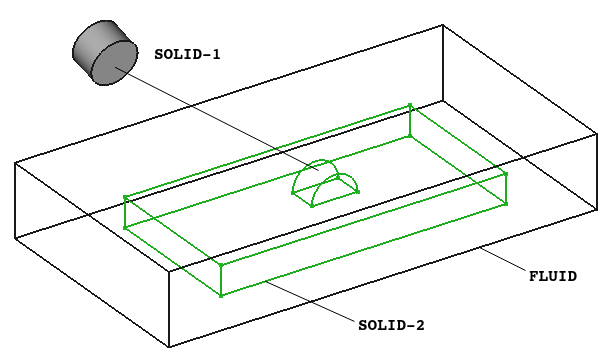
It is not explicitly documented in SCDM user manual in which order the parameters get updated - however it is logical to assume that the parameters shall get updated in the order they are created / stored. And the parameters are stored in the order they are created and not in the order sorted by user say ascending alphabetically. It is better to define parameters with constant reference frame instead of taking reference from any other floating object.
ANSYS WB as in version 2024 does not allow to change the ID of parameters though GUI and they are stored in the order they are created. Parameter ID can be changed by editing the Workbench project file *.wbpj using a text editor. Search for all instances of a parameter which usually is named as P** where ** represents the sequence number (such as P1, P2, P13, P21...) and replace them by the new name (preferably keeping the naming convention same). If parameters have been used in expressions, renaming parameters should take care of keeping this dependency.Few Recommendations for Parametric Modeling
- While deciding the mean, low and high levels of parameters: check the design for limiting conditions which may cause manufacturing or assembly limitations
- Keep all references to measure length with respect to fixed surfaces and/or edges (those which are not affected by geometrical changes
- While moving a round (fillet), use the edge of fillet on the side of straight face - in other words align the "direction of move" and "direction of measurement"
- Create parameters in group and order which does not contradict to subsequent constraints - note that if any parameter definition is missed for a shape, it will come later in the list (sequence of update) and may result in incorrect shape and size
- Keep testing the correctness of parametrization in small chunks (such as group of 10 driving dimensions) - this will help identify the driving dimension(s) causing failure in update of the geometry (create back-up after each successful check)
- Create a simple yet distinct naming convention for driving dimensions such p11_x_h where 1 refers to type 1, next 1 refers to item 1, x refers to direction, [h, w, b..] may refer to the variable names such as height, width, gap...
- In ANSYS SpaceClaim, you cannot change the order of driving dimensions - hence a careful planning is critical, especially all the dimensions required for a particular feature such as protrusions or cut-outs should be in consecutive sequence
- Create parameters responsible for changes in size first followed by parameters or ruler dimensions required for translation of objects
- Organize the variables in DOE table in the similar order (as per the expected sequence of update in CAD environment)
- Do not use default location of 'Move' handle which is near the centroid of the chosen objects, if shape changes the centroid will change and hence translation dimension need to account for this change in centroid position.
- Create 10 ~ 20 geometries manually using parameters randomly selected from the DOE table and overlap them in a single file. This will give a good visual representation of expected changes and error / anomaly in parameter values or definitions.
In general (for a single solid body and not assembly), the order of update of parameters or driving dimension should not matter. If the order of update affects the final shape and size of the body, recheck the input dimension - they might not be correct. For example, some update might have resulted in loss of feature (a face or edge) leading to missing reference for next update. "One or more objects may have lost some scoping attachments during the geometry update" or meshing operation get stuck in batch mode (playing a recorded script) > Very often geometry selections such as Named Selections, zones defined for inflation layer settings, reference edge for move operation... become invalid as the edge or surface referred while creating them do not exist at some values of input parameters.
When a parameter is changed in SCDM, the geometry change is updated but the parameter set value does not update in Workbench parameter set. User the option Update Parameter in SpaceClaim under the 'Workbench' tab which will push the updated value to Parameter set.Using an Excel Spreadsheet to Drive Dimensions
This utility is part of add-ins which can be activated using SpaceClaim Options > Add-ins > (Check the box) Excel Dimension Editor Add-in > Restart SpaceClaim.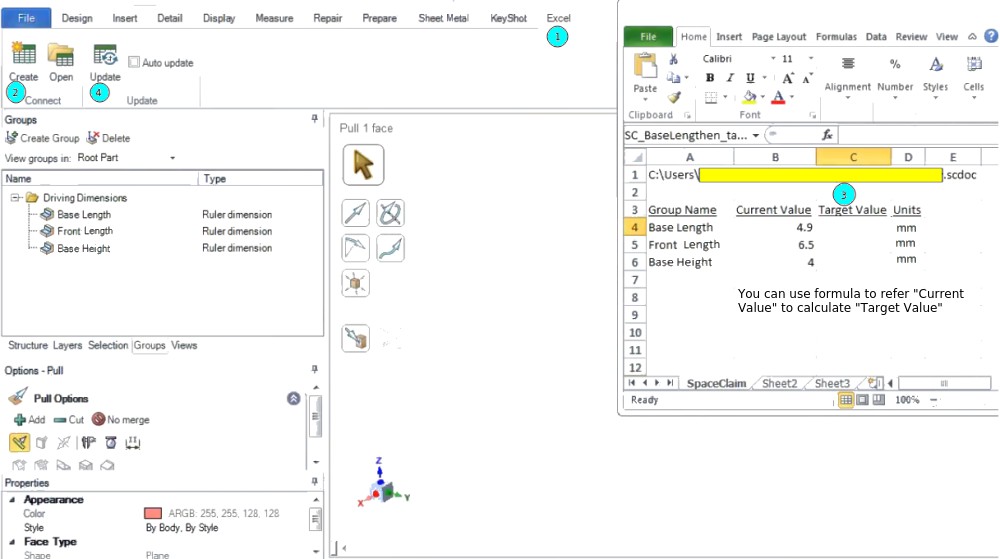
Driving Changes with Annotation Dimensions
3D annotation dimensions can be used to change design using the Pull and Move tools. Annotation dimensions can be used in combination with ruler dimensions. Dimension can be used for every element in design, from lines in sketches to faces of solids. In Discovery SpaceClaim, dimensions are not constraints rather tools for precise control during the creation or modification of a design. To save a dimension with the design, Ruler Dimension option can be used when pulling or moving.Error: File has wrong dimensions (3) > this is usually reported in case 2D geometry is not in XY plane (which Fluent is expecting). By default SpaceClaim draws sketch in XZ plane which needs to be rotated to meet requirement for Fluent pre-processor.
As per innovationspace.ansys.com/ ... /driving-parameter-and-script-parameter:
# Get list of named selections and driving dimensions in Groups tab dims_NS = Window.Groups.GetValue(Window.ActiveWindow) # # 3-tuple type: value is index 1, type is index 2 # Type = (Linear, Angular, Arc, Area, Diametric, Mass, Volume) dims_NS[0].TryGetDimensionValue() dims_NS[0].SetDimensionValue(value)A script to move objects defined by Named Selection is described below (not tested - generated by AI). Note that SCDM recording feature does not capture steps to create ruler dimensions. And hence the ruler dimensions cannot be accessed in Python script - changing ruler dimension is same as executing a 'Move' operation.
import SpaceClaim.Api.V242 as sc
from SpaceClaim.Api.V242 import Point, Direction, DesignPoint
#from SpaceClaim.Api.V242 import *
'''
User Inputs: Named Selections and Move Direction
object_to_move = Named selection for object(s) to move
move_dir_name = Named selection of face/edge to get direction
ref_point_name = Named selection of a vertex or point
move_distance = Distance to move in [mm]
'''
object_to_move = "ns_fillet_x"
move_dir_name = "ns_mmv_dir_1"
ref_point_name = "ns_ref_pnt_1"
ns_move_anchor = "ns_anchor"
move_distance = 50
target_selection = Selection.CreateByGroups(SelectionType.Primary, object_to_move)
move_direction = Selection.CreateByGroups(SelectionType.Primary, move_dir_name)
anchor = Selection.CreateByGroups(SelectionType.Primary, ns_move_anchor)
direction = Move.GetDirectionAlignedTo(target_selection, move_direction)
'''
Other options to create direction are:
direction = Move.GetDirectionAlignedTo(anchor, move_direction)
direction = -Direction.DirZ
mv_face = Selection.CreateByGroups(SelectionType.Primary, ns_mv_face) #face normal
direction = Move.GetDirection(mv_face)
'''
options = MoveOptions()
options.CreatePatterns = False
options.DetachFirst = False
options.MaintainOrientation = False
options.MaintainMirrorRelationships = True
options.MaintainConnectivity = True
options.MaintainOffsetRelationships = True
options.Copy = False
options.SnapAssociatedVertices = True
options.SubProportionalRadius = MM(0)
result = Move.Translate(target_selection, direction, MM(5), options) #IN(0.02)
# Note Move calculates 'change' from current value between anchor and target
# Get direction vector from edge or planar face normal
direction_item = move_direction.Items[0]
if direction_item.ShapeType == sc.ShapeType.Edge:
curve = direction_item.Geometry
direction_vector = (curve.EndPoint - curve.StartPoint).Direction
elif direction_item.ShapeType == sc.ShapeType.Face:
face = direction_item.Geometry
direction_vector = face.Normal
else:
raise Exception("Move Direction must be an edge or planar face.")
reference_point = Selection.CreateByGroups(ref_point_name)
if reference_point and reference_point.Count > 0:
ref_item = reference_point.Items[0]
if hasattr(ref_item, 'Point'):
ref_point = ref_item.Point
else:
ref_point = ref_item.Shape.Geometry.Center
else:
ref_point = Point.Origin # default to origin if not specified
move_vector = direction_vector * move_distance
transform = Transform.CreateTranslation(move_vector)
result = Move.Execute(target_selection, transform)
print(f"Moved '{object_to_move}' by {move_distance} along '{move_direction}'")
def getNamedSelection(ns_name):
select_ns = Selection.CreateByGroups(ns_name)
if not select_ns or select_ns.Count == 0:
raise Exception(f"Named Selection '{ns_name}' not found or empty.")
return select_ns
# Create Driving Dimension as parameter and apply initial transform of 0 [unit]
axis_map = {
"X": coordinate_system.XDirection,
"Y": coordinate_system.YDirection,
"Z": coordinate_system.ZDirection
}
if move_axis not in axis_map:
raise Exception("Invalid move_axis. Choose from 'X', 'Y', or 'Z'.")
selected_axis = axis_map[move_axis]
end_point = ref_point + 1.0 * selected_axis
initial_transform = Transform.CreateTranslation(selected_axis * 0)
Move.Execute(target_selection, initial_transform)
Get summary of dimensions for edges and/or faces
ns_list = GetActiveWindow() .ActiveWindow .Groups
mea_dim = []
for ns in ns_list:
if (ns.GetNames().Contains("msr")):
ns_members = ns.Members
mea_dim.append(ns_members[0].Shape.Length) # Output is in [m]
mea_dim_row = ','.join(mea_dim)
print(mean_dim_row)
From discuss.ansys.com under topic "Extract edge length and export information":
import os
import io
import json
file_path = os.path.join(r"D:\Projects", "edge_lengths.json")
bodies = GetRootPart().GetAllBodies()
body = bodies[0]
edge = body.Edges[0]
e_length = edge.Shape.Length
len_dict = { "edge length" : e_length }
with io.open(file_path, "w", encoding="utf8") as json_file:
json.dump(len_dict, json_file, ensure_ascii=False)
Guidelines to Design Thermal Management System
Following considerations are recommended to design air-cooled and liquid-cooled systems:- The available space and envelope such as inlet and outlet connectors, location of fans... should be as per component placement
- For gas (air) cooled systems:
- The design approach with passive cooling (natural convection) and active cooling (forced convection) are different
- Both may use heat spreader (heat sinks) and thermal interface material
- In passive cooling, the orientation of the part and hence the orientation of heat spreader or heat sink should is along direction of gravity
- For active cooling case, the location of fan should be inline with the heat sink and there should be diverging duct to control the swirl of the fans
- For liquid cooled systems:
- First criteria is to meet the pressure drop requirement (maximum permissible pressure drop) for specified flow rate
- The cooling channel should be in a curved or serpentine shape to cover larger surface area which also ensures continuous mixing of hot and cold fluid (no formation of thermal boundary layer)
- The heat conducting face of heat generating devices (MOSFET, IC, Capacitors...) should be directly mounted on the heat sink or cooling channel plates as per the layout of the components
- Ensure good contact between the heat generating parts and the cooling plate or heat spreader by using thermal grease or thermal interface material (TIM)
- The sizing of the channels are iterative: for cooling channels with Aluminium and copper, the liquid (cooling medium) velocity is limited to 2 [m/s] or 5-8 [ft/s]* and for stainless steel the limit is 4 [m/s]. This is to avoid pitting (erosion) at higher liquid velocities. High water velocity in copper channels can strip the protective copper oxide layers and thus accelerate corrosion-erosion of the channels
- Sometimes a minimum average velocity is also need to be met to avoid fouling and depositions on the channel walls
- The minimum wall thickness is governed by burst pressure requirements. In terms of thermal performance, a lower wall thickness leads to better conductive heat transfer.
| Material | Recommended maximum velocity |
| Low Carbon Steel | 10 ft/sec - 3.0 [m/s] |
| Stainless Steel | 15 ft/sec - 4.5 [m/s] |
| Aluminum | 06 ft/sec - 1.8 [m/s] |
| Copper | 08 ft/sec - 2.4 [m/s] |
| 90-10 Cupronickel | 10 ft/sec - 3.0 [m/s] |
| 70-30 Cupronickel | 15 ft/sec - 4.5 [m/s] |
Naming Convention of Boundaries and Cell Zones
In any practical application of CFD simulations, the computational domain may comprise of many cells zones (fluid and solid zones) and boundary zones (walls, inlets and outlets). The engineer responsible for pre-processing may not be the one who creates solver file and post-processes the results. The reviewer(s) of the mesh and simulation set-up will certainly be not the engineer who created them. In order to convey the domain information seamlessly, a naming convention should be adopted, it can be a generic system applicable for large number of projects or a specific system for particular simulation set-up. An example is outlined below with following default setting: Newtonian, stationary, adiabatic, smooth boundaries or zones can be named arbitrarily though it is recommended to chose names and identifiers meaningfully.- Inlet(s) and outlet(s) should be named as b_inlet_id, b_outlet_id where 'id' stands for identifier.
- Walls with boundary conditions (other than adiabatic): w_tpr_id, w_hfx_id, w_htc_id, w_rot_id w_mov_id, w_rgh_id, w_s2s_id where 'rgh' stands for rough walls, s2s stands for coupled solid walls.
- Cell zones: fld_air_id, fld_wtr_id, fld_oil_id, fld_nnw_id, fld_rot_id, por_mom_id, por_thm_id, sld_alm_id, sld_stl_id, sld_src_id ... where 'nnw' stands for non-Newtonian fluids, 'src' stands for solid zones with heat source and/or sink and 'por' stands for porous (fluid) zones.
- Internal planes: int_f2f_id, int_baf_id ... where 'baf' stands for thin walls or baffles.
- Non-conformal interfaces: if_f2f_id, if_s2s_id, if_sta_rot_id, if_por_fld_id, if_por_por_id where 'sta' stands for 'stationary' zones and 'por' stands for 'porous' zones.
- All boundaries with no special setting or conditions to be applied on them can be named as 'b_def_id' or dumy-id1, dumy-id2 or empt-id1, empt-id2 or fblk-id1, fblk-id2 where dumy stands for dummy, empt for empty and fblk for flow-blockers. This is especially important while dealing with assemblies with large number of solids and fluid zones.
DOMAIN SIZE REDUCTION THROUGH SIMILARITY: In order to results of the model to apply to the prototype, strict similarity rules must be followed.
A convenient frame of reference must be defined that applies to both model and prototype and corresponding locations must be defined using dimensionless ratios (for a sphere for example, angle on its surface, longitude and latitude lines). Thus, there exist similar conditions for corresponding points on both model and prototype. That is, the drag coefficient at a particular point on the sphere applies to both model and prototype.
The designer must follow, then geometric similarity (model and prototype), kinematic similarity (velocity vector direction is similar for both model and prototype), dynamic similarity (force vector direction is similar for both model and prototype), thermal similarity (heat fluxes)...
Note that similarity principles cannot be applied for all application without loss of accuracy. For example, to reduce size of an axial flow fan with shroud, either for numerical or experimental investigation, their is no thumb rule to account for blade-tip and shroud clearance. Hence, the designer has to establish his own "quality standards and acceptance criteria" to address this limitation
Domain size reduction by sub-modelling
Domain size reduction by axi-symmetry
Defeaturing in ANSYS Discovery
The pre-processing activities require geometry simplifications (defeaturing) and ANSYS SpaceClaim has some powerful non-parametric features. One of them is the 'Pull' option (short-cut 'p') which is equivalent to 'sweep' or 'extrude' operation. By default, pull direction is tangent to the selected edge or perpendicular to the selected face. A direction can be chosen or pulled (sweep) along a curve. Selection: all holes equal to selected radius, all holes of same radius in same face, all holes of radius equal or smaller than select radius. Blend (b): create surface by two lines (it is equivalent to 'loft' operation in some CAD programs). Fill (f): create surface from a closed loop of curves. Move (m): the 'origin' option is to select the reference point on the source object.
Step-by-Step for Geometry Defeaturing and Simplifications (ANSYS Spaceclaim)
Step-1:
Split the large assemblies into smaller (if possible, geometrically less-dependent) domain. This helps avoid large memory requirement and further geometry clean-up operations as well.Step-2: Re-group and rename the data
The geometry in CAD environment is created keeping in mind the physical construction and assembly sequences. This is not important in mesh generation. It is better to re-group the geometrical (CAD) entities in terms of expected boundary definition. This makes it easy to operate on a smaller section of the entire domain. The selection, hide/unhide and operations such as imprint/ interference become faster.Step-3:
Further segregate the geometry into 'Solids' and 'Surfaces'. This helps chose operations appropriate for the respective category. Such as fillet removal, split, booleans and extrude (pull) is easy on solids.Step-4:
Convert the solids with thin wall thickness into solids with no internal wall and void. For example, a beam with fillets and internal wall.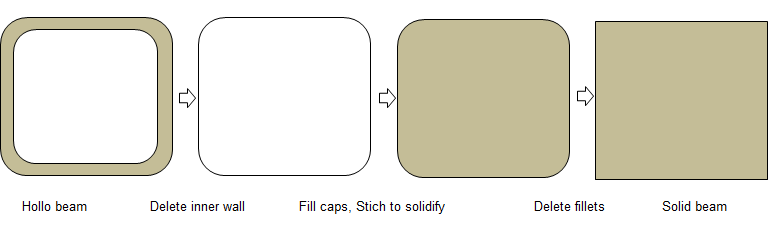
Step-5:
Before removing the wall thickness, use the operations appropriate for solids such as Booleans like unite, intersect... to make sure the once converted to surface, no further operations such as extend /intersection is needed to remove the gaps / connect the surfaces. Note that this method is no recommended for FEA simulation. in CFD the blockage of flow is important where as in FEA the location of centroid is important. 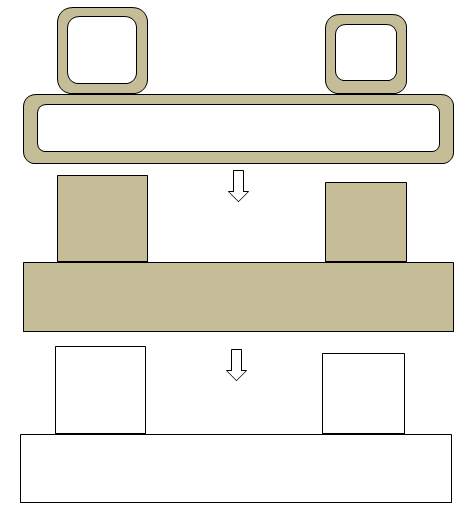
Step-5:
ANSYS Spaceclaim is a CAD-type pre-processor and works better on solids. CFD volume extraction is a analogous to 'negative' of visible solid volumes. Instead of deleted the unwanted surfaces one-by-one, it is recommended and worth trying to create a "bounding box" enclosing the geometry and use a booleaan to subtract the solids from the 'bounding' box. The resultant negative volume of fluid domain is easy to operate and remove the protrusions generated due to gaps in original (input) geometry.SpaceClaim has versatile feature called Pull operation which can be used to extrude faces and edges, create fillets and chamfer and remove materials. Tangent and Natural (curvature continuous) extension can be toggled when dragging the end of a curve. To drag the extension Tangent to the curve, press and hold Ctrl prior to dragging. Press 'Ctrl' and drag to 'Pull' the curve end tangent to the curve. Surface edges can be Pulled normal to their neighbouring face. Press the Ctrl key when you begin the Pull. Press Ctrl and drag to Pull the edge tangent to the surface. Pulling a face with its edges selected extrudes the face without influence from neighbouring faces. Pulling a conical face "Up To" a parallel cylindrical face replaces the cone with the cylinder if the axes are close together. Otherwise, the conical face is replaced with a cylindrical face that is coaxial to the cone and has the same radius as the cylinder.
Tips and Tricks:
Definition: gaps in the plane of a surface is called lateral (horizontal) gaps and gaps in the direction of area normal is called the transverse (vertical) gap.
If you are dealing with large surfaces with small (transverse) gaps (say < 1% of the biggest geometry or say 1-5 [mm] which you can neglect), follow these steps:
- Create a plane and/or planar surface encompassing the entire geometry which defines the best possible horizontal plane for the lower bound of the geometry.
- Extend (using 'extrude', 'sweep' or 'pull' tool) by amount which covers (fills) all the unevenness (transverse gaps) in the geometry.
- Split the bodies (solid volumes and surfaces) as per appropriate tool. E.g. in ANSYS SpaceClaim, "Split Body" can be used for both solid and surface bodies. 'Split' tool can be used for surfaces only.
- This process will remove the 'local' details such as 'openings', small surfaces or patches for named selection... Project the curves from original geometry as needed and then split the bigger surfaces created during previous operations.
- Delete the unwanted extensions created due to 'extend' and 'trim / split' operations.
- Repeat the process for other bodies in the assembly.
- Repeat the process for the upper and left / right bounds of the geometry. Though, once the lower and upper bounds are flattened (made coplanar), the 'blend' and 'fill' operation can be used to fill any lateral gaps between vertical edges and surfaces.
Fill operation: selecting many contiguous (connected) surfaces for fill operation does not work. However, selecting just one surface out of many makes the 'fill' tool act nicely. If 'fill' operation does not work while removing fillets and rounds, use Delete Rounds under Prepare > Remove > Rounds. Many a times, the sequence of fill operation determines the success of operation especially when fillets of different radii are connected in a loop. One need to visualize that the deletion of a fillet or blend should result in valid geometry.
Do not 'stitch' the geometry body and surfaces until you are done with all necessary clean-up and simplifications.
'Imprint' and 'Interference' operations do not make intended change in on go. Continue the operation till you get a message "No problem areas were fixed".
In ANSYS SpaceClaim, sometimes 'pull to' operation does not work. However, you can manually 'pull' or 'extend' the edges to or beyond the desired target edge. Hence, extend the edges manually and split them later to have a common boundary. Another option is to copy the surface(s) into a new model file and then do pull / fill / trim operations. Once desired shape is achieved, copy-paste the new geometry or shape back into main assembly.
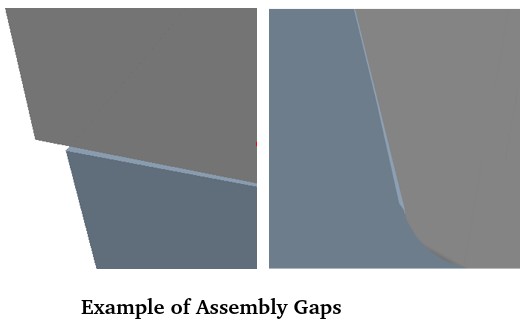
Sometimes, the edges of the surfaces forming the gaps are short and split into many segments. Most of the geometry defeaturing programs have option to Fit Curves. However, this operation may not work if curves are already associated with surface. In ANSYS SpaceClaim, Patch Fill is another option. First click on Fill Ribbon tool without selecting any geometry. Under the options, the default is Extend Fill. Change the option to Patch Fill. If any geometry was previously selected, it would have extended fill.
Split Geometry for Meshing
Many a times, it is a necessity to split the geometry appropriately into multiple volumes especially when this sections are present. Such splits are required to create extrudable or sweepable sections to generate either full hexahedral mesh or use thin sweeping method to generate all prism elements in narrow gaps. Splitting a body with plane is straightforward though the options to split a (solid) body with a curved plane (surface) is more frequently needed. ANSYS Discovery provides Combine operation to split solids using other solids or surfaces. In the image below where two cylinders are merged, a full cylindrical surface needs to be created (say for the vertical cylinder). This surface can be used to split the two cylinders into separate bodies.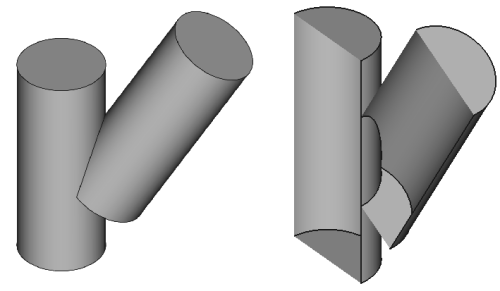
ANSYS Discovery has option to save all the components into separate files. Select the components, right-click and chose Convert to External. The icon for the component in the Structure tree changes to indicate 'external'. A batch converter converter.exe located in the install directory of Discovery can be used to convert files to other formats.
If the bodies are stored without components, directly under root components, select the bodies which needs to be saved in separate files, right click and chose "Move Each to A Component". This will move each body in separate components and the steps mentioned earlier can now be used to save them into separate files. Discovery has different type of components: internal, external, dependent and independent.
How to compare two geometry when external appearance look similar? One way is to check the surface area - the one with higher value is expected to have bigger cross-section and lengths. This can be further confirmed by comparing the volumes of the two geometries.
Data Exchange among MCAD / ECAD Tools
Navisworks (from AutoDesk) is primarily a mesh-based program, which uses polygon models to represent 3D objects. These mesh models are efficient for visualization but lack the precision and scalability of NURBS (Non-Uniform Rational B-Splines) or solids-based models used in MCAD tools. In Navisworks Simulate or Manage, export the NWD file to the FBX format. Read the FBX file in Blender and export it into STL format. Navisworks is an (intermediate) viewer and reviewer of 3D models, not to create or source of 3D models like other MCAD tools (Creo, SolidWorks, CATIA...).
Blender Tool for Geometry Clean-up
Blender is not a CAD modelling program. For example, there is no concept of solids even if it is enclosed from all sides by faces, the concept of Boolean (add, subtract...) in Blender is not same as standard 3D CAD tools. Note that you can extrude a face and the operation is named as Solidify. Since Blender works on tessellated geometries, they are 'hollow' or "empty inside" by definition. The attributes such as mass or matter inside an object, centre of gravity... cannot be assigned to objects in Blender.Other products offering similar features are Maya 3D (AutoDesk 3d Max or 3D Studio) and Houdini. From the website of Autodesk: "What is Maya? Maya is professional 3D software for creating realistic characters and blockbuster-worthy effects. Bring believable characters to life with engaging animation tools. Shape 3D objects and scenes with intuitive modelling tools. Create realistic effects – from explosions to cloth simulation." From the official page of Houdini: "Houdini is built from the ground up to be a procedural system that empowers artists to work freely, create multiple iterations and rapidly share workflows with colleagues. In Houdini, every action is stored in a node. These nodes are then “wired” into networks which define a “recipe” that can be tweaked to refine the outcome then repeated to create similar yet unique results. The ability for nodes to be saved and to pass information, in the form of attributes, down the chain is what gives Houdini its procedural nature."
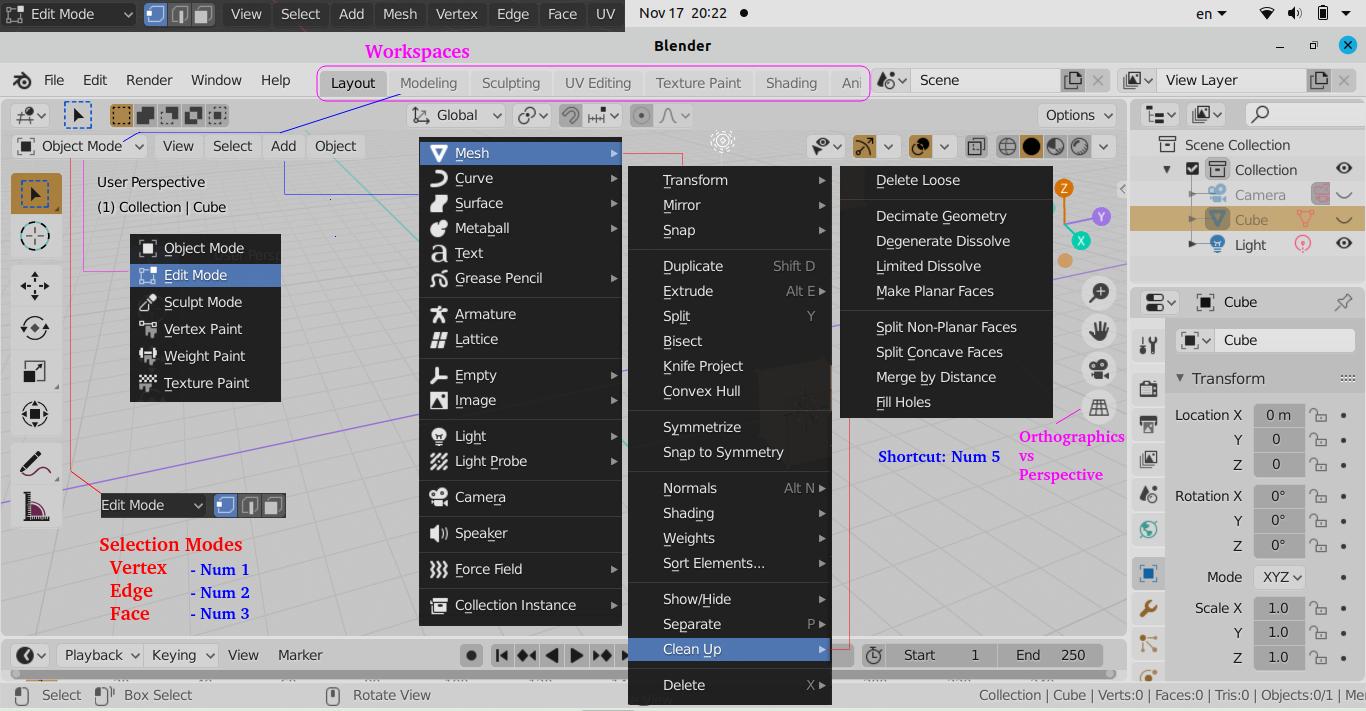
Like many feature rich applications, the interface of Blender is a bit intimidating (complex and lost in ocean type) when you open it the first time. Understaing the GUI layout and context based sub-menu is key to get started.
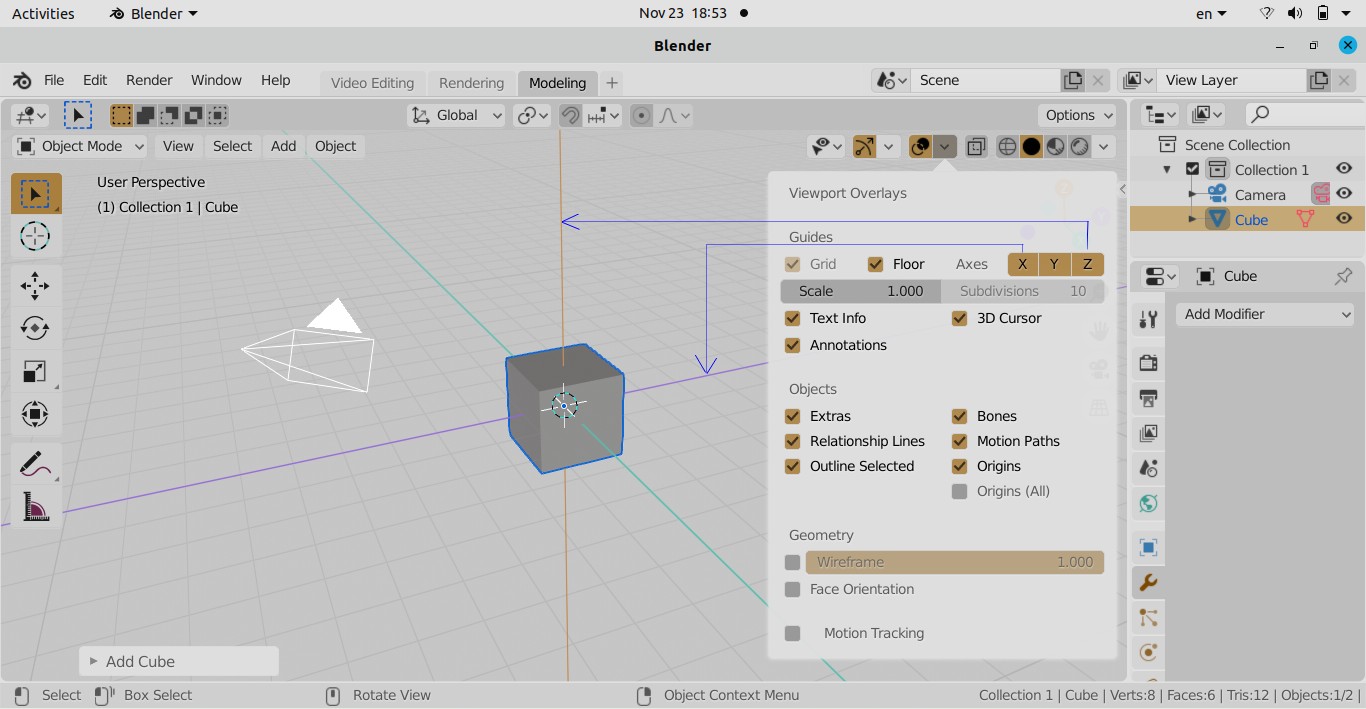
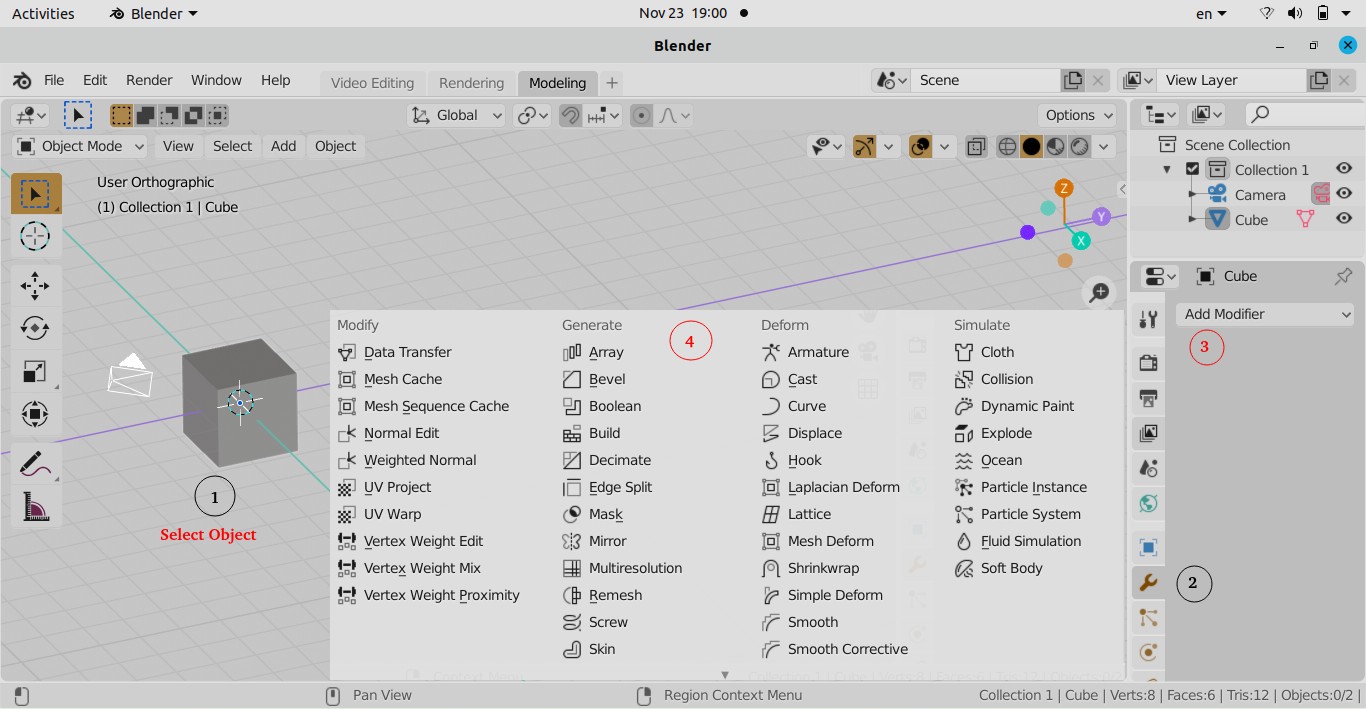
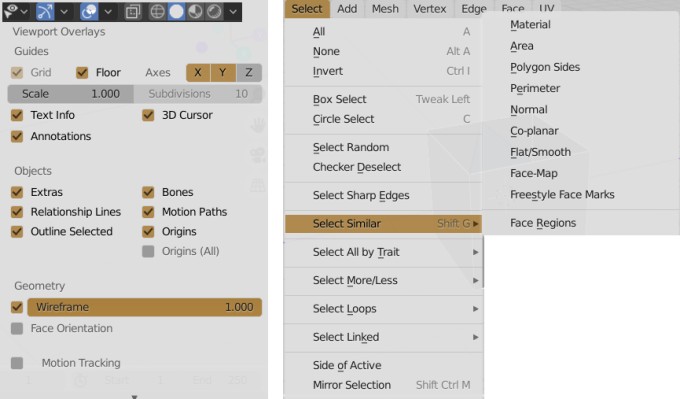
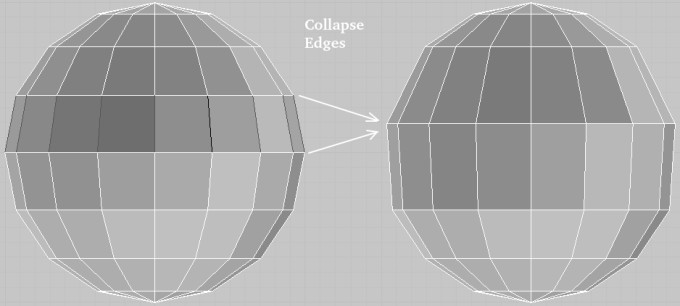
Fix for Viewport Clipping
Also known as object cut-off issue, zooming in to inspect texture or mesh details in 3D view clips faces partially like a clipping mask not showing the full model. Click on the small left arrow (< sign) on the top right near XYZ-triad to open the following pane.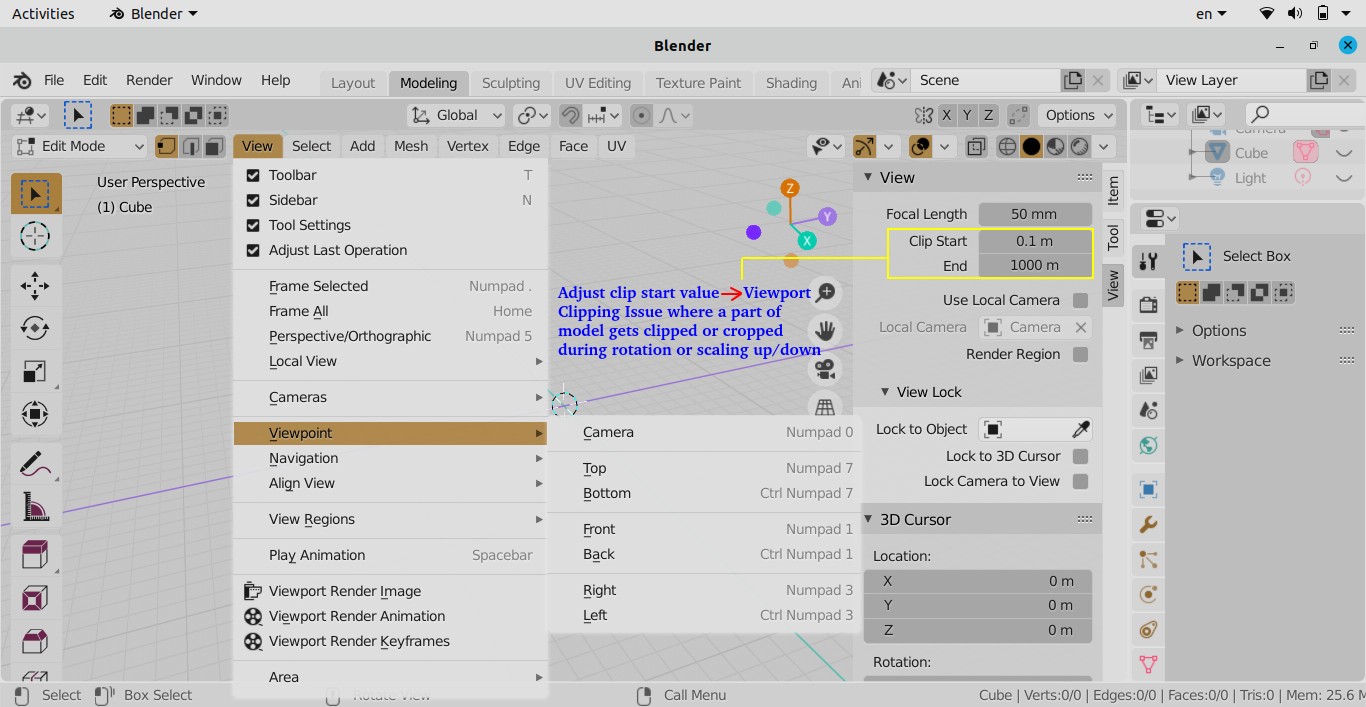
Some challenges dealign with tessellated geometries are removing fillets and chamfers from imported say STL file, deleting coincident surfaces (common boundaries of two closed volumes), removing proximities at sharp corners and point contacts such as a tire contacting flat ground.
ANSYS Discovery (known as SpaceClaim and DesignSpark) has on option called Vectorize Image that creates curves around colored areas in images. This can be used to create a 2D domain from images. A colour convention can be use to define domain and material types (solid, fluid, insulator...).
Curves
A curve or segment of a curve is defined as collection of points whose coordinates are specified as continuous ONE-parameter and single-valued mathematical functions. In Cartesian coordinate system, it can be expressed as x = f(u), y = g(u) and z = h(u) where f, g and h are the single valued mathematical functions. 'u' is known as parametric variable and it is very often (and necessarily) constrained to the interval [0 1]. The curves are said to be point-bounded as it has two definite end points.Linear parametric equation of curves: x = a + b.u, y = m + n.u, z = p + q.u where a, b, m, n, p and q are constants. The curves starts at p(u=0) = [a m p] and ends as [(a + b) (m + n) (p + q)] with direction cosines proportional to b, n and q.
Cubical parabola: x = a.u, y = b.u2, z = c.u3 where a, b and c are constants.
Left-handed circular helix: Also known as machine screw, the curves are described as x = r.cos(u), y = r.sin(u), z = p.u where r and p are constants. It is the locus (path) of a point that revolves around the z-axis at radius r and moves parallel to the z-axis at a rate proportional to the angle of revolution 'u' (known as pitch of the helix). Note that if p < 0 then it is a right-handed screw (helix).
All the 3 examples above demonstrate the versatility of parametric representation of a curve. However, we need to always have a independent variable (u or θ) as parameter. Even, x or y or z themselves can be a parameter so that x=f(x), y=g(x) and z=h(x). Similarly, the surfaces can be represented parametrically. This is the reason the 3D CAD geometry in SolidWorks, Unigraphics, Creo, Inventor, FreeCAD... are called parametric models and the method is called parametric modelling.Algebraic Form of a Parametric Cubic (PC) Curve: Following 3 polynomials are required to define any curve segment of a PC curve:
x(u) = a0 + a1u + a2u2 + a3u3
y(u) = b0 + b1u + b2u2 + b3u3
z(u) = c0 + c1u + c2u2 + c3u3
The unique set of 12 constant coefficients are known as algebraic coefficients and determines the size, shape and position of the curve in space.Geometric Form of a Parametric Cubic (PC) Curve: Algebraic coefficients do not lend much flexibility to control the shape of a curve in modelling situations as they do not account for conditions as its ends points or boundaries. When a curve is described based on its conditions as the ends (such as end point coordinates, tangents, curvature, torsion...), it is called geometric form of the curve.
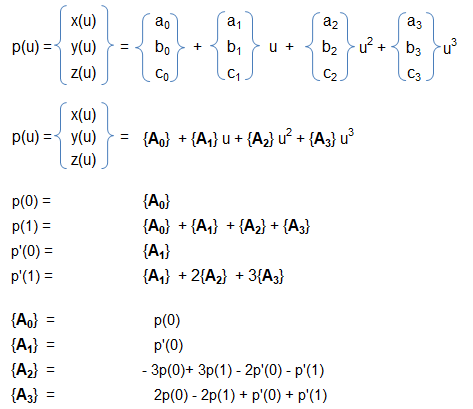
STEP/IGES
STEP (or STP) and IGES (or IGS) are two widely used neutral file format. IGES format was developed in 1980 by US Air Force in collaboration with Boeing, GE and Xerox. STEP format came into existence in 1984 as ISO standard 10303-21. Both these standards are plain text formats that use pre-defined special purpose syntax. For example, entity names in STEP format consists of digits preceded by '#'. /* ... */ defines comment. STEP format does not maintain features such as fillets, chamfers... as separate geometrical entities.Create Periodic Planes
The easiest option is to cut the geometry with two planes inclined at desired sector angle and passing through the axis of rotation. This option any cut through the blades (rotating as well as stationary) through the domain shall still remain periodic by definition.
Another approach is to draw a plane passing between two adjacent blades, the plane need not pass through exactly middle point of the leading edges. Create another plane inclined to the first plane at required sector angle. Split the geometry by these planes.
The following method is similar to previous one except 5 to 8 planes may be required to split the geometry into axial and tangential directions.
CAD Data Exchange
STEP format is widely used in data exchange between CAD and numerical (FEA / CFD) simulations. It has many flavours known as AP: Application Protocol. Meta data such as surface names are included when using the STEP AP214. Most of the CAD programs including Siemens NX do not include surface names in a STEP (AP 242) export by default but they do have option to make the surface names included while using AP 214 of STEP format.Similarly, to define 'names' in PTC Creo, the design can use: File > Prepare > Open Model Properties, then select 'Names' in the model properties dialogue. Then select faces by clicking > enter a name in the dialogue box opened in previous step. During CAD export to STEP format with default settings, the 'names' defined earlier do not get stored in the file. Change the export setup through File > Options > Configuration Editor > intf_out_assign_names > set it to 'user_name'.
Scripting in ANSYS Discovery / SpaceClaim
The main prerequisite is the familiarity with SpaceClaim GUI and nomenclature. Other than the official User Guide, a short and detailed resource is the appendix in the book "Computational Fluid Dynamics: An Introduction to Modeling and Applications, 1st Edition" from McGraw Hill. The appendix on SpaceClaim can be found at "accessengineeringlibrary.com/content/book/9781264274949/back-matter/appendix5". Few examples of scripts can be found at github.com/inr-kit/SpaceClaim_scripts. It uses IronPython which in turn uses .NET framework. The Python API is found in <ANSYS_INSTALL_DIR> v212\ scdm\ SpaceClaim .Api .V212\ API_Scripting_Class_Library.chm --Also, "discuss.ansys.com/categories/3d-design" is a good source of help and sample codes. Many of the codes on this page are either a copy or adaption of codes posted on this website.
To open SpaceClaim in batch mode: "C:\Program Files\ANSYS Inc\v232\scdm\SpaceClaim.exe" /Welcome=False /Splash=False /RunScript="E:\Projects\geo_script.py" /ExitAfterScript=True /Headless=True where geo_script.py should contain IronPython script. "%awp_root241%\Discovery\Discovery.exe" --hidden -o Geo.dsco --run-script "E:\Prj\scr.py" --exit-after-script
Read a *.scdoc file using Pyhton following by running a Python script. Reference: post titled "how-to-use-code-open-scdm-scdoc-file" at discuss.ansys.com
current_dir = os.path.dirname(os.path.realpath(file)) #os.getcwd(): get the installation folder of SCDM / Discovery #GetActiveWindow().Document.Path: get the path of currently loaded geometry geo_file = "Project.scdoc" scr_file = "geo_Script.py" geo_path = os.path.join(current_dir, geo_file) scr_path = os.path.join(current_dir, scr_file) with open(geo_path, 'r') as scdm_file: geo_content = scdm_file.read() with open(scr_path , 'r') as py_file: scr_content = py_file.read()
The SCDM / Discovery files are referred as Document. To open a file: File.Open(r "E:\Projects\Design-1.dsco"). To save it: DocumentHelper .GetActiveDocument() .Save(). To save as: DocumentHelper .GetActiveDocument() .SaveAs(r "E:\Projects\New.dsco")
It is important to know definitions of terms in SCDM such as 'Part', 'Body', 'Component', 'Surface'... A body with faces that form a closed (watertight) volume is considered a solid. Bodies whose faces do not 'close' fully are considered as surface bodies. Solid bodies and surface bodies can be distinguished by the icons before their names in the GUI. The Python script window in SCDM has autocomplete property of built-in variables and methods. A drop-down appears once you type the dot separator. To get properties and methods associated with a given SpaceClaim object, use Dir() command. For example, Dir(face .Edges[0] .Shape .Geometry) will give list of all properties and methods inside face .Edges[0] .Shape .Geometry.
Get the root part: part = GetRootPart(), bodyNames = GetRootPart() .GetAllBodies() or bodies = GetRootPart() .GetChildren[IDesignBody](), Get all named selections: groups = GetActiveWindow() .ActiveWindow .Groups. Such lists can be accessed by standard "for loop" in Python such as "for bd in bodyNames:" or "for ns in groupsNS:". To select all faces of a body: bd_faces = bd.Faces where bd is defined as a body earlier. To get name of a body: bd_name = bd.GetName().
Orient view in isometric direction in spaceclaim: ViewHelper.ActivateNamedView('Isometric',True). Other options for view names are ['Trimetric', 'Top', 'Bottom', 'Left', 'Right', 'Front', 'Back']
Get all components: compList = GetRootPart() .GetAllComponents(). Make a component independent (break association with instance array): makeIndep = ComponentHelper .MakeIndependent(compName, None). Get Instance Suffix of a component name: c_name = compName.Name, Get searchable name of a component: q_name = compName.GetName() - notice the parentheses. Rename a component: compName.setName( new_comp_name ). Rename a body: bd_name.SetName( new_body_name ). Get all bodies in a component: body_list_in_comp = compName.GetAllBodies(). Get number of bodies in a component, Note that Selection.Create(body) creates a selection of 'body' and not creates the 'body':bodies = part.GetAllBodies() n_body = body_list_in_comp.Count. face_body_1 = Selection.Create(bodies[1].Faces)To select all bodies: select = Selection.SelectAll() or
part = Window.ActiveWindow.Document.MainPart select = Selection.Create(part.Bodies)Create components and activate one
comp_01 = ComponentHelper.CreateAtRoot("comp_01")
comp_02 = ComponentHelper.CreateAtRoot("comp_02")
comp_11 = ComponentHelper.CreateAtComponent(comp_01, "comp_11")
ComponentHelper.SetActive(comp_11.CreateComponents[0])
Change "Share Topology" properties of a Component:
comp = GetRootPart().Components[3] comp.Content.ShareTopology=comp.Content.ShareTopology.Share
Get components by excluding names from a list
def selectComponentsExludeNames(exclude_names, only_root_comps=False):
comps = []
if (only_root_comp):
comps = GetRootPart().Components
else
comps = GetRootPart().GetAllComponents()
comp_list = []
for comp in comps:
if comp.GetName() not in exclude_names:
comp_list = comp_list.append(comp)
return comp_list
#Usage:
exclude_names = ["hsrc_fpga", "heat_sink"]
comp_list = selectComponentsExludeNames(exclude_names, True)
Set the .stl import unit system: options are Millimeters, Meters, Inches
file_stl = 'E:\surf_import.stl' from SpaceClaim.Api.V232 import * un = MetricUnits(MetricLengthUnit.Millimeters, MetricMassUnit.Kilograms, AngleUnit.Degrees) importOptions = ImportOptions.Create() importOptions.Stl.Units = un DocumentOpen.Execute(file_stl, importOptions)
Variables can be derived through the Insert Selection (the button with the black arrow and the small green '+' symbol in the script editor). Codes related to visibility and selections: Select and invert selection --- select = Selection.GetActive() .ViewHelper .ShowAll(), result = ViewHelper.InvertVisibility().
Make faces opaque: selection = BodySelection.Create( list_of_bodies ). ColorHelper .SetFillStyle( selection, FillStyle.Default, FillStyle .Opaque).Select all faces of part, faces using index values, body and datum planes:
PartSel = Selection.Create(GetRootPart()) faces = PartSel.ConvertToFaces() Selection.Create(GetRootPart().Bodies[0].Faces[0]) Selection.Create(GetRootPart().Bodies[0]) datumSel = Selection.Create(GetRootPart().DatumPlanes[0])
Select faces by bounding box - selects faces if they are even partially inside the bounding box: innovationspace.ansys.com/ ... /spaceclaim-script-selection-by-filterbyboundingbox
PartSel_1 = Selection.Create(GetRootPart()) Faces_1 = PartSel_1.ConvertToFaces() PartSel_2 = Selection.Create(GetRootPart().Bodies[0]) Faces_2 = PartSel_2.ConvertToFaces() Faces = Selection.Difference(Faces_1, Faces_2) BBox = Box.Create(minX, minY, minZ, maxX, maxY, maxZ) Faces_in_BB = Faces.FilterByBoundingBox(BBox)
Smart Selection
selection = PowerSelection .Faces .ByRoundRadius(Face1, PowerSelectionOptions(False), SearchCriteria .SizeComparison .SmallerOrEqual, SearchCriteria .RoundType .All)secondarySelection = Selection.Empty()
options = FillOptions()result = Fill.Execute(selection, secondarySelection, options, FillMode.ThreeD, Info1)
Codes related to body and components such as select, move, rename, add to components:
selection = Body1 result = ComponentHelper.MoveBodiesToComponent(selection, Info1) result = RenameOject.Execute( selection, "Part_X") selections = Body2 result = ComponentHelper .MoveBodiesToComponet(selections, Component, False, Info2).
Create named selections: w_hflux is the name of the list containing faces selected based on certain criteria.
result = NamedSelection.Create(Selection.Create( w_hflux ), Selection())
result = NamedSelection.Rename("Group1", "w_heat_flux")
primarySelection = FaceSelection.Create(GetRootPart().Bodies[1].Faces[1])
secondarySelection = Selection.Empty()
result = NamedSelection.Create(primarySelection, secondarySelection)
result = NamedSelection.Rename("Group1", "w_faces_fixed_t")
Create a named selection by using FilterByArea:
part = Selection.Create( GetRootPart())
face_list = comp.ConvertToFaces().FilterByArea(minArea, maxArea)
face_list.CreateAGroup("w_fillets")
Create named selection based on volume:
def createNSbyVolume(minVolume, maxVolume):
shapesByVol = []
assembly = GetRootPart()
bodies = assembly.Bodies
for body in bodies:
# Check for solid body and ignore surface bodies
if (body.GetMaster().Shape.IsClosed == True):
shape = body.Shape
volume = shape.Volume
if (volume >=minVolume and volume <=maxVolume):
shapesByVol.append(body)
return shapesByVolSelect all rounds and fillets ≤ given radius and create separate named selections for concave and convex shapes. PowerSelection method has option to filter depending on convex or concave shape. In its current form, this script searches for rounds in all available bodies.
rad = 2.5
select_convex =
PowerSelection.Faces.ByRoundRadius(MM(rad),
PowerSelectOptions(False, BodySelection.Create(GetRootPart().GetAllBodies())),
SearchCriteria.SizeComparison.SmallerOrEqual,
SearchCriteria.RoundType.Convex)
select_convex.SetActive()
result = NamedSelection.Create(select_convex, Selection.Empty())
result.CreatedNamedSelection.SetName("convex_faces")
select_concave =
PowerSelection.Faces.ByRoundRadius(MM(float(UserRadius.Value)),
PowerSelectOptions(False, BodySelection.Create(GetRootPart().GetAllBodies())),
SearchCriteria.SizeComparison.SmallerOrEqual,
SearchCriteria.RoundType.Concave)
select_concave.SetActive()
result = NamedSelection.Create(select_concave, Selection.Empty())
result.CreatedNamedSelection.SetName("concave_faces")
Selection.Clear()
Get faces aligned with specified direction and also located on the 'top' of the body in that direction.
user_direction = Direction.DirZ
//Change this to UserDirection = Direction.DirX, or any arbitrary direction
//with XYZ like Direction.Create(0.50, 0.75, 1.25)
dot_tolerance = 0.9999
top_faces = []
for body in GetRootPart().GetAllBodies():
z_faces = []
for face in body.Faces:
face_normal = face.GetFaceNormal(0, 0)
dot_product = Vector.Dot(face_normal.UnitVector, UserDirection.UnitVector)
if dot_product > dot_tolerance:
z_face = face.GetFacePoint(0, 0)[2]
z_faces.append([face, z_faces])
if len(z_faces) > 0:
z_faces.sort(key=lambda V: V[1])
top_faces.append(z_faces[-1][0])
Selection.Create(top_faces).SetActive()
Operation on all bodies containing a string
bodyNames = GetRootPart().GetAllBodies()
bd_names_uniq = set(bodyNames)
uniq_names_list = list(nd_names_uniq)
for bd in bodyNames:
bd_name = bd.GetName()
bd_faces = bd.Faces
# Create named selections
ns_name = "w_" + bd_name
Selection.Create(bd_faces).CreateAGroup(ns_name)
if (bd_name.Contains("source")):
... do something ...
# Loop over faces of a body. x_cg = cg[0], y_cg=cg[1]
for face in body.Faces:
cg = face.MidPoint().Point
ViewHelper.ShowAll()
ns_groups = Window.ActiveWindow.Groups
To create unique names of bodies in a (root) part, following code can be used.
names_list = ['Mango', 'Banana', 'Guava', 'Mango', 'Grapes', 'Mango']
def createUniqList(names_list):
size_list = len(names_list)
names_uniq = set(names_list)
# Convert unique names back to a list
uniq_list = list(names_uniq)
for uniq_item in uniq_list:
n_repeat = names_list.count(uniq_item)
i = 1
if (n_repeat > 1):
for itr in range(size_list):
if (names_list[itr] == uniq_item):
names_list[itr] = uniq_item + "_" + "{:02d}".format(i)
i = i + 1
return names_listNamded Selection on Faceted Bodies
mesh_comps = GetRootPart().Meshes
dir_vector = Vector.Create(1, 0, 0)
mesh_comp_items = []
for mesh_comp in mesh_comps:
for face in mesh_comp.Shape.Faces:
normal = face.Normal.UnitVector
dir_cosine = Vector.Dot(dir_vector, normal)
if (dir_cosine >= 0.9):
mesh_comp_items.append(mesh_comp.GetDesignMeshTopology(face))
if (len(mesh_comp_items) > 0):
Selection.Create(mesh_comp_items).CreateAGroup("faceted_faces")
Create shapes: radSph = 100, sphBody.Create( Point.Create(MM(0), MM(0), MM(0)), Point.Create(MM(radSph), MM(radSph), MM(0)), ExtrudeType .None), x1 = 10, y1 = 25, x2 = 50, y2 = 75. Create line:
start = Point2D .Create(MM(x1), MM(y1)) end = Point2D .Create(MM(x2), MM(y2)) result = SketchLine.Create(start, end)
Get normal at given uv point of a face: normal_uv = faces[3].GetFaceNormal(0.4, 0.6)
Create point on an edge and inside a facept_edge_perc = faces[0].Edges[3].EvalProportion(0.25).Point DatumPoint.Create(GetRootPart(), "pnt_", pt_edge_perc) pt_u_v = faces[1].EvalProportion(0.25, 0.75).Point pt_u_v = faces[1].GetFacePoint[0.50, 0.25]Create lines:
line_12 = Line.CreateThroughPoints(p1, p2) crv_nurbs = NurbsCurve.CreateThroughPoints(False, "pnt", 0.001) crv_segment = CurveSegment.Create(crv_nurbs) design_crv = DesignCurve.Create(GetRootPart(), crv_segment) DatumLine.Create(GetRootPart(), "line_", line_12)Create Cuboid from Two Diagonally Opposite Corners where dimensions are in [m]:
p1 = Point.Create(x0, y0, z0) p2 = Point.Create(x0 + Lx, y0 + Ly, z0 + Lz) result = BlockBody.Create(p1, p2, ExtrudeType.ForceIndependent)Create Circular Face:
circ_normal = Direction.DirY circ_centre = Point.Create(0, 0, 0) circle = CircularSurface.Create(circ_rad, circ_normal, circ_centre)
Create a Torus using circle created above:
pt_origin = Point.Origin pt_z = Direction.DirZ rot_axis = Line.Create(pt_origin, pt_z) x_section = Selection.Create(circle.CreateBody.Face[0]) RevolveFaces.Execute(x_section, rot_axis, DEG(360), RevolveFaceOptions())Create Cylinder:
result = CylinderBody.Create(p1, p2, p3, ExtrudeType.ForceIndependent) cyl_body = result.CreatedBodyor
def createCylinderBody(base_point, end_point, radius): direction = (end_point - base_oint).Direction.ArbitraryPerpendicular pt3 = end_point + (direction.UnitVector * radius) result = CylinderBody.Create(base_point, end_point, pt3)Copy and Translate:
trans_vector = Vector.Create(dx, dy, dz) result = Copy.Execute(Selection.Create(base_body)) new_body = result.CreatedObjects[0] Move.Translate(Selection.Create(new_body), trans_vector, MoveOptions())
Extrude Face and Edge
selection = Face1 options = ExtrudeFaceOptions() options.extrudeType = ExtrudeType.Add result = ExtrudeFaces.Execute(selection, MM(5), options, Info1) selection = Edge1 secondarySelection = = Axis1 #Global X-axis options = ExtrudeEdgeOptions() result = ExtrudeEdges.Execute(selection, secondaryselection, MM(20), options, Info2)
Create a sketch plane and point on that plane: plane = Plane.ZX, result = ViewHelper .SetSketchPlane(plane), point = Point2D .Create( MM(x1), MM(y1) ), result = SketchPoint .Create(point)
Change to Solid View mode: mode = InteractionMode .Solid, result = ViewHelper .SetViewMode(mode). Set Section View: sectionPlane = Plane .PlaneXY, result = ViewHelper .SetSectionPlane(sectionPlane). Create Datum Plane: plane = Plane.PlaneYZ, result = DatumPlaneCreater .Create(plane, False).
Create Datum Point and 1D/2D Patterns
selection = CoordinateSystem1 result = DatumPointCrestor.Create(selection, 0, 0, False, Info3) selection = DatumPoint1 data = LinearPatterndata() Get.PatternDinension = PatternDimensionType.Two #Remove this line for 1D pattern data.LinearDirection = Axis1 data.CountX = 2 data.PitchX = 5 data.CountY = 3 #Remove this line for 1D pattern data.PitchY = 8 #Remove this line for 1D pattern result = Pattern.CreateLinear(selection, data, Info4)
Ref: innovationspace.ansys.com/ ... /discovery-spaceclaim-scripting-examples: scripts to (a) loop through bodies and its faces to identify face midpoint, compare it with center coordinates of inlet and outlet (b) create Named Selection groups – inlet, outlet, wall and fluid, by identifying the faces (inlet, outlet) based on their location.
Delete unwanted edges: SCDM/Discovery has built-in option to delete unwanted edges. However, to remove edges from specific shapes only:
sph_edges = sph_comp.GetAllBodies()[0].Edges #sph_edges = sph_comp.GetAllBodies()[0].GetDescendants[IDesignEdge]() edges_sph = Selection.Create(sph_edges) Delete.Execute(edges_sph)
Codes to repair geometry and Share Topology:
result = FixInterference .FindAndFix(Info1)
result = FixSplitEdges .FindAndFix()
result = FixExtraEdges .FindAndFix(Info2)
options = FixMissingfacesOptions()
result = FixMissingFaces .FindAndFix(options, None)
result = FixImprint.FindAndFix()
options = ShareToplogyOptions()
options .Tolerance = MM(0.05)
result = ShareToplogy .FindAndFix(options, Info3)
# Create NS of the shared faces
options = ShareTopologyNamedSelectionOptions()
options.Tolerance = MM(0.10)
ShareTopologyNamedSelection.FindAndFix(options)
# Get all groups created during Share Topology operation
Connectgroups = Window.ActiveWindow.Groups
Merge Bodies: targets = BodySelection .Create(Body1), tools = BodySelection .Create(Body2), result = Combine .Merge( targets, tools ). Define material: mat_name = GetRootPart() .Bodies[0] .Material
Get Geometry Information: Get area of a face - bd_faces[0]. bd_faces[0].Shape.Perimeter, bd_faces[1].Edges.Count, By selecting edges the vertices defining the edge can be accessed. bd_faces[2].Shape.Geometry.GetType() - get type of face such as cylinder or plane. Get centroid of a face: GetRootPart( ).Bodies[1] .Faces[2] .EvalMid( ).Point.
Get face normal: GetRootPart( ).Bodies[0] .Faces[1] .GetFaceNormal(0, 0)
Get radius: face.Edges[0] .Shape .Geometry .Radius
or
face.Edges[0] .Shape .GetGeometry[Circle]() .Radius
Get mid-point: face .MidPoint() .Point
Get centre of an edge: edge.Shape .GetGeometry[Circle]() .Axis .Originvol = body .MassProperties .RawSubject or vol = body.Shape .Volume cen = vol.Center.Faces.AdjacentFaces edge = face.Shape .Edges[i] face.Shape .GetAdjacentFace(edge) Faces[i].Edges .Count Faces[i].GetTangentChain().CountTo get the common face between two bodies, all the faces have to be iterated on one body and parent(s) of each faces should be checked. If the two bodies share a face, use body[i].Faces to get the faces of a body and face[j].Bodies to get the bodies attached to faces. The face which has two bodies attached to it is the connecting face. If the two bodies do not share the same face (e.g. share topology operation should be avoided for some reason), but have two faces that are identical, loop through all the faces on each body and find the ones that have common centroids. Third option is to create named selection during Share Topology operation and loop through the faces in the NS Group. GetRootPart() .Bodies[i] .Faces[j] .Parent returns the return the Idesignbody associated with a face.
Get the face(s) closest to a given point where coordinates are specified in milli-meters and faces are searched in X-direction.
def facesClosestToPoint(p_x, p_y, p_z):
pt = Point.Create(MM(p_x,), MM(p_x,),MM(p_x,))
direction = Direction.DirX
rayOrigin = pt + direction.UnitVector * (-0.001)
face_list = RayFire.Fire(rayOrigin, direction, 1.0E-10, 1.0E-5)
for face in face_list:
if (isinstance(face, IDesignFace)):
Selection.Create(face).CreateAGroup("facesClosest")
break
Get number of total faces: numFaces = len(GetRootPart() .Bodies[0] .Faces). Get normal: norm_value = str((GetRootPart() .Bodies[0] .Faces[i] .GetFaceNormal(0, 0))). Compare normal direction of a surface with +x direction: norm_value == 'Direction: (1, 0, 0)'. Get all edges of a body: GetRootPart() .Bodies[0] .Edges, Get Z-coordinate of start point of an edge: z0 = GetRootPart() .Bodies[0] .Edges[1] .Shape .StartPoint .Z, Create a datum plane aligned to zx-plane: datumPlane = DatumPlaneCreator .Create(Point .Create(0, y0, 0), Direction.DirY) .CreatedPlanes[0]
Rotate a body about Y-axis:selection = Body1 anchor = CoordinateSystem1 axis = Move.GetAxis(anchor, HandleAxis.Y) options = MoveOptions() result = Move.Rotate(selection, axis, DEG(30), options, Info1)To access first local coordinate system: cs_loc = GetRootPart().CoordinateSystems[0], to get origin: origin_cs = cs_loc.Frame.Origin --Any other coordinate system can be refered with CoordinateSystems[i] where i = 1, 2, 3...
Get centroid of a surface of a solid body, not surface bodies. Note that instances of solid bodies are known as 'DesignBody' and instances of surface bodies are called 'IDesignBody'. Thus, IsClosed property exists in the Shape property of the DesignBody and not in the instances of IDesignBody. Method-1: mass_prop = bodies[1].MassProperties .RawSubject, cen_body_1 = mass_prop.Center. Method-2: refer the code below.
selected_items = Selection.GetActive().Items
for selected_item in selected_items:
if not isinstance(selected_item, DesignFace):
continue
#if isinstance(selected_item, DesignFace):
# or
#is_solid = selected_item.GetMaster().Shape.IsClosed
sel_i = Selection.Create(selected_item)
pt = MeasureHelper.GetCentroid(sel_i)
new_pt = SketchPoint.Create(pt)
Get mass properties: principal axes and moments about principal axes. Ref: discuss.ansys.com/ ... /how-to-get-the-combined-space-claim-mass-properties
body_list = BodySelection.Create(GetRootPart().Bodies) massProps = MeasureHelper.GetMassProperties(body_list) mass = massProps.Mass pa_x = massProps.PrincipleAxes.AxisX pa_y = massProps.PrincipleAxes.AxisY pa_z = massProps.PrincipleAxes.AxisZ principalMomentXAxis = massProps.GetMoment(pa_x) principalMomentYAxis = massProps.GetMoment(pa_y) principalMomentZAxis = massProps.GetMoment(pa_z) pa_x_dir = pa_x.Direction pa_y-dir = pa_y.Direction pa_z_dir = pa_z.Direction
Get centre of a body
bodyProp = GetRootPart().Bodies[0].MassProperties bodyCenter = bodyProp.PrincipleAxes.Origin XC = bodyCenter.X YC = bodyCenter.Y ZC = bodyCenter.Z
Bounding box: returns two diagonally opposite corners.
BBox = GetRootPart().Bodies[0].Shape.GetBoundingBox(Matrix.Identity) bodyCenter = BBox.Center corners = BBox.Corners corner1 = corners[0] corner1_X = corner1.X
Get centroid of all bodies defined in Named Selection
groups = GetActiveWindow().ActiveWindow.Groups
for ns in groups:
ns_name = ns.GetName()
ns_members = ns.Members
for member in ns_members:
if (isinstance(member, DesignBody):
mass_prop = member.MassProperties.RawSubject
centre = mass_prop.Center
print(centre[0], centre[1], centre[2])Set Material Type: ref = discuss.ansys.com/ ... /how-can-i-assign-a-material-to-multiple-bodies-in-spaceclaim
mat = GetRootPart().Bodies[0].Material matId = SpaceClaim.Api.V24.MaterialPropertyId prop = SpaceClaim.Api.V24.MaterialProperty(matId.ElasticModulus, "Elastic Modulus", 15, None) mat.SetProperty(prop) mat_name = "Gray Cast Iron" succ_local, local_mat = Window.ActiveWindow.Document.Materials.TryGetValue(mat_name) if not succ_local: succ, mat = SpaceClaim.Api.V24.LibraryMaterial.Library.TryGetValue(mat_name) local_mat = SpaceClaim.Api.V24.DocumentMaterial.Copy(Window.ActiveWindow.Document, mat) for body in GetRootPart().GetAllBodies(): body.Material = local_mat
Create surface from points: SCDM has a built-in method to create list of geometry objects such as pnt_list = List[Point](), pnt_pair = List[TuplePoint, Point]](), crv_list = List[ITrimmedCurve]() or pnt_list = List(Tuple[Point, Point]](). Here .Add method is used to add items and not .Append
Ref: discuss.ansys.com/discussion/2294/create-a-surface-from-multiple-points
from System import Tuple
ClearAll()
p_x = [0 5 10 20 25]
p_y = [5 10 15 20 25]
p_z = [10 15 20 25 30]
n_pt = len(p_x) - 1
points = []
for i in range (n_pt)
p_name = "p" + str(i)
p_name = Point.Create(p_x[i], p_y[i], p_z[i]
points.append(p_name)
list_points = List[Tuple[Point, Point]](Tuple.Create(points[i-1], points[i]) for i in range(len(points)))
list_curves = CurveSegment.Create(list_points)
d_curves = []
for curve in list_curves:
curve = DesignCurve.Create(GetRootPart()
d_curves.append(curve)
result = Fill.Execute(Selection.Create(d_curves))
surface = Selection.Create(result.CreatedFaces[0])
Delete.Execute(Selection.Create(d_curves))crv_list = List[ITrimmedCurve]() p1 = Point.Create(x1, y1, z1) p2 = Point.Create(x2, y2, z2) curve = CurveSegment.Create(p1, p2) crv_list.Add(curve) ... # Create surface through the curves result = PlanarBody.Create(Plane.PlaneXY, crv_list) bd = result.CreatedBody # Extrude to create a body dir = Direction.Create(0, 0, 1) face = Selection.Create(bd.Faces[0]) ExtrudeFaces.Execute(face, dir, MM(2.5), ExtrudeFaceOptions()) ViewHelper.ZoomToEntity()Alternatively: Point cloud can be imported into SpaceClaim as curves where order of coordinates in a text file is Z X Y. fit=true to fit a smooth spline through the points instead of straight line segments. polyline=false to create each curve as separate entity. A newline is required after every point data row. Go to Assembly and click on the File+ button. Select the text file formatted as described below.
3d=true polyline=true fit=false Z0 X0 Y0 Z1 X1 Y1 ... Zn Xn Yn
Create washers on all bolt holes in all bodies:
hole_edges = Selection.Create(bodies).ConvertToEdges().ConvertByShape(GeometryType.Circle)
min_rad = 5.0
max_rad = 10.0
extrude_h = 2.5
for edge in hole_edges:
if edge.Items[0].Shape.Geometry.Radius > MM(min_rad) and
edge.Items[0].Shape.Geometry.Radius < MM(max_rad) :
selection = edge
direction = MoveImprintEdges.GetImprintDirection(edge, edge.ConvertToFaces()
.ConvertByShape(GeometryType.Plane), False)
options = MoveImprintEdgeOptions()
result = MoveImprintEdges.Execute(selection, direction, MM(extrude_h), options)
extrude_faces = List[IDesignFace]()
list_faces = Selection. Create(GetRootPart().GetAllBodies()).ConvertToFaces()
.ConvertByShape(GeometryType.Plane)
for face in list_faces:
edges = face.ConvertToEdges()
if (edges.Count == 2):
extrude_faces.Add(face.Items[0])
Selection.Create(extrude_faces).CreateAGroup("ExtrudedFaces")Sample Scripts from Public Domains and discuss.ansys.com
Basic Operations: Open / Save / Import - 'Window' lass refers to the graphical interaction window showing part a part or a drawing sheet.
ClearAll()
File.Open(r"E:\Sctipts\Bracket.dsco") # Open Project, Document.Open(file_name)
DocumentOpen.Execute(r"E:\Projects\Case_1.scoc", FileSettings1)
impOpt = ImportOptions.Create()
DocumentOpen.Execute(r"E:\Projects\Case_1.scoc", impOpt)
GetActiveWindow().Close # Close currently opened window
Window.Close(GetActiveWindow()) # Close active window
# If the window being closed is the last window of the document and needs
# saving, the user will not be prompted to save changes.
DocumentHelper.CloseDocument()
# convert CAD files and save them in the same directory
import glob, os
os.chdir(r"E:\Scripts\")
for file in glob.glob("*.stp"):
File.ResetProject()
File.Open(os.path.join(os.getcwd(), file), ImportOptions.Create())
File.SaveAs(os.path.join(os.getcwd(), file[:-4]+".igs"))
# Run Discovery script in batch mode
"C:\Program Files\Ansys Inc\v221\Discovery\Discovery.exe" --run-script \
"E:\Scripts\pipe.scscript" --hidden --exit-after-script
# Save Project As
File.SaveAs(r"E:\Scripts\U-Bracket.dsco")
Run Discovery script from WB project page
import os geo_file = "E:\Scripts\pipe.scscript" #SetScriptVersion(Version="22.1.217") template = GetTemplate(TemplateName="Geometry") system = template.CreateSystem() geometry = system.GetContainer(ComponentName="Geometry") geometry.Edit(IsDiscoveryGeometry=True) geometry.RunScript(ScriptFile=geo_file, GeometryContainer="Geometry", useAsMacro="false") geometry.Exit()
Create Objects and Bodies
datumPlane = DatumPlaneCreator.Create(Point.Create(0, 0, planeZ), Direction.DirZ) .CreatedPlanes[0]
def createPlaneOriginNormal(origin = [0, 0, 0], normalDirection = [0, 0, 1]):
originPoint = Point.Create(origin[0], origin[1], origin[2])
dirZ = Direction.Create(normalDirection[0], normalDirection[1], normalDirection[2])
frame = Frame.Create(originPoint, dirZ)
plane = Plane.Create(frame)
return plane
def getGroup(groupName):
groups = GetActiveWindow().ActiveWindow.Groups
for group in groups:
if group.GetName() == groupName:
return group
return None
def getDimensionValue(group):
tryGetDimensionResult = group.TryGetDimensionValue()
if tryGetDimensionResult[0]:
return True, tryGetDimensionResult[1]
else:
return False, 0
def setDimensionValue(group, value):
group.SetDimensionValue(value)
# Fill
selection = Face1
secondarySelection = Selection.Empty()
options = FillOptions()
result = Fill.Execute(selection, secondarySelection, options, FillMode.ThreeD, Info1)
# Thicken Faces
selection = FaceSelection.Create(Face0, Face1, Face2, Face3)
options = ThickenFaceOptions()
result = ThickenFaces.Execute(selection, Direction.Create(0.707, 0, 0.707), MM(-5), options)
# Create Rounds
selection = PowerSelection.Edges.ByLength(Edge1,
PowerSelectOptions(True), SearchCriteria.SizeComparison.Equal)
options = ConstantRoundOptions()
result = ConstantRound.Execute(selection, MM(2.5), options, Info1)
# Create a block
startPoint = Point.Create(MM(5), MM(5), MM(15))
endPoint = Point.Create(MM(20), MM(20), MM(20))
BlockBody.Create(startPoint, endPoint)
# Create rectangles
RectangularSurface.Create(MM(40), MM(5),Point.Origin)
RectangularSurface.Create(MM(5), MM(40),Point.Origin)
# Merge rectangles
allSurfaceBodies = PowerSelection.Bodies.AllSurfaceBodies()
result = Combine.Merge(allSurfaceBodies)
# Create a plane and switch to sketch mode
origin = [MM(5), MM(5), MM(5)]
plane = create_a_plane_from_origin_and_normal(origin)
ViewHelper.SetSketchPlane(plane)
# Sketch Spline
points = List[Point2D]()
points.Add(Point2D.Create(MM(0), MM(15)))
points.Add(Point2D.Create(MM(5), MM(5)))
points.Add(Point2D.Create(MM(15), MM(0)))
result = SketchNurbs.CreateFrom2DPoints(False, points)
splineCurve = result.CreatedCurves[0]
# Switch to 3D mode
mode = InteractionMode.Solid
ViewHelper.SetViewMode(mode)
# Extrude spline
selection = Selection.Create(splineCurve)
options = ExtrudeEdgeOptions()
result = ExtrudeEdges.Execute(selection, Point.Origin, Direction.DirZ, MM(30), options)
resultFace = result.CreatedFaces
## Slice block by resultFace
toolFaces = Selection.Create(resultFace)
selection = PowerSelection.Bodies.AllSolidBodies()
result = SplitBody.ByCutter(selection, toolFaces, True)
sel_body = Selection.Create(GetRootPart().Bodies[0])
sel_datum = Selection.Create(datum_plane)
SplitBody.Execute(sel_body, sel_datum)
# delete unncessary bodies
referencePoint = Point.Create(MM(5), MM(5), MM(15))
for body in GetRootPart().GetAllBodies():
if not body.Shape.ContainsPoint(referencePoint):
body.Delete()
# Extrude resulting surface body
faceToExtrude = result.GetModified[IDesignFace]()
faceToExtrudeSelection = Selection.Create(faceToExtrude)
options = ExtrudeFaceOptions()
options.ExtrudeType = ExtrudeType.Add
result = ExtrudeFaces.Execute(faceToExtrudeSelection, MM(40), options)
# Create the named selections
Selection.Create(GetRootPart().Bodies).CreateAGroup("SolidBody")
for face in GetRootPart().Bodies[0].Faces:
if (face.Shape.ContainsPoint(Point.Create(MM(2.5), 0, MM(2.5)))):
Selection.Create(face).CreateAGroup("Fixed support")
if (face.Shape.ContainsPoint(Point.Create(0, MM(2.5), MM(2.5)))):
Selection.Create(face).CreateAGroup("Pressure load")
#How to Access Groups
groups = GetActiveWindow().ActiveWindow.Groups
for group in groups:
print group.GetName()
#How to get all items of a Group/Named Selection
group = GetActiveWindow().ActiveWindow.Groups[0]
Group.Members
#or
Selection.CreateByGroups("Height").Items
heightGroup = getGroup("Height")
tryGetDimensionResult = heightGroup.TryGetDimensionValue()
print(tryGetDimensionResult)
Get and Set Dimension Values
for group in groups:
if not group.HasDimension:
group.Delete()
topGroup = getGroup("Top")
tryGetDimensionResult = topGroup.TryGetDimensionValue()
print(tryGetDimensionResult)
heightGroup = getGroup("Height")
success, height = getDimensionValue(heightGroup)
if success:
print(height)
heightGroup.SetDimensionValue(MM(5))
if success:
print(height)
setDimensionValue(heightGroup, height + MM(4))
Using script parameter to create a surface
Test = Parameters.Test
RectangularSurface.Create(Test, Test, Point.Origin)
#Units of Script Parameters
Length = Parameters.Length
myUnits = UnitsHelper.GetDocumentUnits()
print("Parameter - SI units: " + str(Parameters.Length))
print("Parameter - local units (" + myUnits.LengthProperties.Type.ToString() \
+ "): " + str(Parameters.Length*myUnits.LengthFactor))
#Set radius2 to initial value minus radius1 divided by 3
r1Group = getGroup("radius1")
success, radius1 = getDimensionValue(r1Group)
r2Group = getGroup("radius2")
success, radius2 = getDimensionValue(r2Group)
if success:
print(radius2)
setDimensionValue(r2Group, radius2 - radius1/3)
Objects, Selections and Named Selections
#Access Bodies: select bodies using part.Bodies
Selection.Clear()
part = GetRootPart()
bodies = part.Bodies
selection = Selection.Create(bodies)
selection.SetActive()
#Access Bodies: select bodies using part.GetBodies()
part = GetRootPart()
bodies = part.GetBodies()
selection = Selection.Create(bodies)
#select bodies using part.GetBodies(“filter”)
part = GetRootPart()
bodies = part.GetBodies("_2")
selection = Selection.Create(bodies)
#listing bodies using part.GetAllBodies()
part = GetRootPart()
bodies = part.GetAllBodies()
for body in bodies:
print(body.GetName())
#Index of bodies
part = GetRootPart()
bodies = part.GetAllBodies()
for index,body in enumerate(bodies):
print(index,body.GetName())
# Access Components:
part = GetRootPart()
for component in part.Components:
print(component.GetName())
part = GetRootPart()
for component in part.GetAllComponents():
print(component.GetName())
# Access Coordinate System:
part = GetRootPart()
for coordinateSystem in part.CoordinateSystems:
print(coordinateSystem.GetName())
for coordinateSystem in part.Components[0].GetCoordinateSystems():
print(coordinateSystem.GetName())
for coordinateSystem in part.Components[0].GetAllCoordinateSystems():
print(coordinateSystem.GetName())
for coordinateSystem in part.GetDescendants[ICoordinateSystem]():
print(coordinateSystem.GetName())
# Access Datum Plane
part.DatumPlanes
part.Components[0].GetDatumPlanes()
part.Components[0].GetAllDatumPlanes()
# Access Datum Lines
part.DatumLines
part.Components[0].GetDatumLines()
part.Components[0].GetAllDatumLines()
# Access Datum Points
part.DatumPoints
part.Components[0].GetDatumPoints()
part.Components[0].GetAllDatumPoints()
Setting colour of faces
Colour names can be defined in a list: clr_list = [ColorHelper.Magenta, ColorHelper.Blue, ColorHelper.Cyan, ColorHelper.Red, ColorHelper.Azure]# Getting Faces of body:
bd_list = GetRootPart().Bodies[0]
for face_i in bd_list.Faces:
geo_type = face_i.Shape.Geometry
if isinstance(geo_type, Cone):
ColorHelper.SetColor(Selection.Create(face_i), ColorHelper.Azure)
if isinstance(geo_type, Plane):
ColorHelper.SetColor(Selection.Create(face_i), ColorHelper.Olive)
if isinstance(geo_type, Cylinder):
ColorHelper.SetColor(Selection.Create(face_i), ColorHelper.Violet)
selection = BodySelection.Create(GetRootPart().Components[0].Content.Body[0]))
options = SetColorOptions()
options.UseAlpha = True
options.Exact = True
options.RandomColor = False
options.RandomSeed = 0
options.EdgeColorTarget = EdgeColorTarget.Body
options.FaceColorTarget = FaceColorTarget.Body
ColorHelper.SetColor(selection, options, Color.FromArgb(255, 255, 0, 128))
# Change colour of surfaces
i=0
for body in GetRootPart().GetAllBodies():
if body.Master.Shape.IsClosed==False:
thick=body.GetMidSurfaceAspect().GetThickness()
if thickness.has_key(thick)==False:
thickness[thick] = clr_list[i]
i = i + 1
ColorHelper.SetColor(Selection.Create(body), SetColorOptions(), thickness.get(thick))
# Change colour of parts of type Beam
from SpaceClaim.Api.V212 import PartType
i=0
for item in GetRootPart().Components:
part = item.Content.GetMaster()
if part.Type == PartType.BeamProfile:
beam_profiles[part]=color[i]
i = i + 1
for beam in GetRootPart().GetDescendants[IBeam]():
'''
sect = beam.GetMaster().SectionSource
if beam_profiles.has_key(sect)==False:
beam_profiles[sect]=color[i]
i = i + 1
'''
ColorHelper.SetColor(Selection.Create(beam), SetColorOptions(),
beam_profiles.get(beam.GetMaster().SectionSource))
# Getting Descendants
bd_list = GetRootPart().Bodies[0]
edge_list = bd_list.GetDescendants[IDesignEdge]() #IBeam
selection = Selection.Create(edge_list)
selection.SetActive()
# Getting newly created entities:
bd_list = GetRootPart().Bodies[0]
edge_list = bd_list.GetDescendants[IDesignEdge]()
selection = Selection.Create(edge_list)
options = ConstantRoundOptions()
result = ConstantRound.Execute(mySel, MM(1), options)
selection = Selection.Create(result.CreatedFaces)
ColorHelper.SetColor(mySelection, ColorHelper.Cyan)
cfaces = result.CreatedFaces
length_cfaces = len(cfaces)
# Getting Modified entities
bd_list = GetRootPart().Bodies[0]
edge_list = bd_list.GetDescendants[IDesignEdge]()
sel = Selection.Create(edge_list)
options = ConstantRoundOptions()
result = ConstantRound.Execute(sel, MM(1), options)
selection = Selection.Create(result.CreatedFaces)
ColorHelper.SetColor(selection, ColorHelper.Cyan)
selection = Selection.Create(result.GetModified[IDesignFace]())
ColorHelper.SetColor(selection, ColorHelper.Magenta)
# Operating on Object lists
body_list = GetRootPart().GetAllBodies()
Selection.Create(body_list).SetActive()
body_list.Remove(GetRootPart().GetAllBodies()[1])
Selection.Create(body_list).SetActive()
body_list.Remove(GetRootPart().GetAllBodies()[2])
Selection.Create(body_list).SetActive()
body_list.Add(GetRootPart().GetAllBodies()[1])
Selection.Create(body_list).SetActive()
Selecting entities using Power Selection
sel_0 = Selection.GetActive()
for body in sel_0.GetItems[IDesignBody]():
print(body.GetName())
sel_1 = Selection.CreateByNames("Cylinder")
sel_1.SetActive()
Selection.Clear()
sel_1.GetInverse().SetActive()
sel_2 = Selection.CreateByGroups("Top")
sel_2.SetActive()
sel_3 = Selection.CreateByNames("Box")
sel_3.AddToActive()
sel_4 = Selection.SelectAll()
sel_4.SetActive()
sel_5 = mySel_4 - mySel_3
sel_5.SetActive()
# gets the current selection from the active view
sel_6 = Selection.GetActive()
# create inverted selection
sel_7 = mySel_1.GetInverse()
# select objects from this selection in active view
sel_8.SetActive()
# Power Selection
seedSelection = Selection.CreateByNames("b07")
powSelection = PowerSelection.Bodies.ByVolume(seedSelection,
PowerSelectOptions(True),
SearchCriteria.SizeComparison.SmallerOrEqual)
powSelection.SetActive()
seedSelection = Selection.CreateByNames("b08")
powSelection = PowerSelection.Bodies.ByVolume(seedSelection,
PowerSelectOptions(False),
SearchCriteria.SizeComparison.SmallerOrEqual)
powSelection.SetActive()
# Power Selection – selecting other bodies
otherBodies=Selection.Create(GetRootPart().GetAllBodies())
options=PowerSelectOptions(False, otherBodies)
seed=Selection.Create(GetRootPart().GetAllBodies("b03"))
pSel=PowerSelection.Bodies.ByVolume(seed, options, \
SearchCriteria.SizeComparison.LargerOrEqual)
pSel.SetActive()
otherBodies=Selection.Create(GetRootPart().GetBodies())
options=PowerSelectOptions(False, otherBodies)
seed=Selection.Create(GetRootPart().GetAllBodies("b04"))
pSel=PowerSelection.Bodies.ByVolume(seed, options, \
SearchCriteria.SizeComparison.LargerOrEqual)
pSel.SetActive()
# Power Selection – selecting seed
options=PowerSelectOptions(True,None,True)
seed=Selection.Create(GetRootPart().GetAllBodies("b07"))
pSel=PowerSelection.Bodies.ByVolume(seed, options, \
SearchCriteria.SizeComparison.SmallerOrEqual)
pSel.SetActive()
options=PowerSelectOptions(True,None,False)
seed=Selection.Create(GetRootPart().GetAllBodies("b07"))
pSel=PowerSelection.Bodies.ByVolume(seed, options, \
SearchCriteria.SizeComparison.SmallerOrEqual)
pSel.SetActive()
# Multiple Objects Selection
b1 = GetRootPart().Bodies[0]
b2 = GetRootPart().Bodies[1]
b3 = GetRootPart().Bodies[2]
# Approach 1
s1 = Selection.Create(b1, b2, b3)
# Approach 2
body_list = [b1, b2]
body_list.Add(b3)
s2 = Selection.Create(body_list)
# Approach 3
list = List[IDesignBody]()
list.Add(b1)
list.Add(b2)
list.Add(b3)
s3 = Selection.Create(list)
# Approach 4
s4 = Selection.Create(b1, b2)
s4 = s4 + Selection.Create(b3)
s4.SetActive()
# Mixed Selections
b1 = GetRootPart().Bodies[0]
b2 = GetRootPart().Bodies[1]
b3 = GetRootPart().Bodies[2]
f1 = b3.Faces[0]
f2 = b3.Faces[1]
# Approach 1
s1 = Selection.Create(b1, b2, f1, f2)
# Approach 2
b_list = [b1, b2]
f_list = [f1, f2]
s2 = Selection.Create(b_list + f_list)
s2.SetActive()
# Multiple objects selection
b1 = GetRootPart().Bodies[0]
b2 = GetRootPart().Bodies[1]
b3 = GetRootPart().Bodies[2]
f1 = b3.Faces[0]
f2 = b3.Faces[1]
b_list = [b1, b2]
f_list = [f1, f2]
sel1 = Selection.CreateByObjects([b1, f_list])
sel2 = Selection.CreateByObjects([b_list, f_list])
sel3 = Selection.Create(b1, f1, f2)
sel3.SetActive()
Creating Named Selections
for face in GetRootPart().Bodies[0].Faces:
ns = NamedSelection.Create(Selection.Create(face), Selection())
if isinstance(face.Shape.Geometry, Cylinder):
ns.CreatedNamedSelection.SetName("sideWall")
elif face not in Selection.CreateByGroups("inlet").GetItems[IDesignFace]():
ns.CreatedNamedSelection.SetName("outlet")
else:
ns.CreatedNamedSelection.Delete()
ns = NamedSelection.Create(Selection.CreateByNames("cylinder"), Selection())
nsName = ns.CreatedNamedSelection.GetName()
NamedSelection.Rename(nsName, "cylinder_faces")
Selection.Create(GetRootPart().Bodies[0]).CreateAGroup("cyl_faces")
part = GetRootPart()
for component in part.Components:
bodies = component.GetAllBodies()
selection = Selection.Create(bodies)
selection.SetActive()
# Move bodies to root component
result = ComponentHelper.MoveBodiesToComponent(selection, part, False)
# Delete Empty Components
ComponentHelper.DeleteEmptyComponents(part)
Selection.Clear()
body_list = List[IDesignBody]()
part = GetRootPart()
for body in part.GetAllBodies():
if body.Shape.Volume <= 3e-07 :
body_list.Add(body)
Selection.Create(body_list).SetActive()
tolerance = 3e-7
for body in GetRootPart().GetAllBodies():
if body not in GetRootPart().GetBodies():
ComponentHelper.MoveBodiesToComponent(Selection.Create(body),\
GetRootPart().Root)
for comp in GetRootPart().GetAllComponents():
ComponentHelper.DeleteEmptyComponents(Selection.Create(comp))
powerSel = PowerSelection.Bodies.ByVolume(tolerance, None, \
SearchCriteria.SizeComparison.SmallerOrEqual)
powerSelInv = Selection.Create(GetRootPart().GetAllBodies())-powerSel
result = ComponentHelper.MoveBodiesToComponent(powerSel)
result.CreatedComponents[0].SetName("smallBodies")
result = ComponentHelper.MoveBodiesToComponent(powerSelInv)
result.CreatedComponents[0].SetName("bigBodies")
Creating cylinders by extruding surfaces
ClearAll()
Diameter = [10, 30, 20, 40, 60]
Length = [50, 75, 25, 10, 60]
z_offset = 100
# cylinder creation version 1
for i in range(len(Diameter)):
face_i = CircularSurface.Create(Diameter[i]/2,
Direction.DirZ,
Point.Create(0, 0,
sum(Length[:i])-Length[0] + z_offset)).CreatedBody.Faces
options = ExtrudeFaceOptions()
options.ExtrudeType = ExtrudeType.ForceIndependent
result = ExtrudeFaces.Execute(Selection.Create(face_i), Length[i], options)
result.CreatedBodies[0].SetName("Cylinder_v1_"+str(i))
Selection.Clear()
ViewHelper.ZoomToEntity()
# Solidify Sketch
mode = InteractionMode.Solid
result = ViewHelper.SetViewMode(mode)
# Demo 2
# cylinder creation version 2
for i in range(len(Diameter)):
CenterBottom=Point.Create(0, (sum(Length[:i]) - Length[0]) + z_offset, 0)
CenterTop=Point.Create(CenterBottom.X,
CenterBottom.Y + Length[i], CenterBottom.Z)
DragPoint=Point.Create(Diameter[i]/2.,
CenterTop.Y, CenterTop.Z)
result=CylinderBody.Create(CenterBottom,
CenterTop, DragPoint, ExtrudeType.ForceIndependent)
result.CreatedBodies[0].SetName("Cylinder_v2_"+str(i))
Selection.Clear()
ViewHelper.ZoomToEntity()
# Solidify Sketch
mode = InteractionMode.Solid
result = ViewHelper.SetViewMode(mode)
#Demo 3
ClearAll()
from math import tan, pi
ConeHeight=0.02
ConeAngle=DEG(30)
ViewHelper.SetSketchPlane(Plane.PlaneXY)
pt1 = Point2D.Create(0, 0)
pt2 = Point2D.Create(0, ConeHeight)
pt3 = Point2D.Create(ConeHeight*tan(ConeAngle/2), 0)
SketchLine.Create(pt1, pt2)
SketchLine.Create(pt2, pt3)
SketchLine.Create(pt3, pt1)
result=ViewHelper.SetViewMode(InteractionMode.Solid)
sel = Selection.Create(result.CreatedBodies[0].Faces)
axis = Line.Create(Point.Origin,Direction.DirY)
options = RevolveFaceOptions()
options.ExtrudeType = ExtrudeType.Add
RevolveFaces.Execute(sel, axis, DEG(360), options)
Selection.Clear()
ViewHelper.ZoomToEntity()
# Demo 4
ClearAll()
pt1=Point.Origin
pt2=Point.Create(MM(10), MM(2), MM(2))
result=BlockBody.Create(pt1, pt2, ExtrudeType.Add)
b0=result.CreatedBody
for i in range(10):
sel = Selection.Create(b0)
direction = Direction.DirY
options = MoveOptions()
options.Copy = True
result = Move.Translate(sel, direction, (i+1)*MM(10), options)
Selection.Clear()
ViewHelper.ZoomToEntity()
# Demo 5
ClearAll()
pt1=Point.Create(MM(-10),MM(0),MM(0))
pt2=Point.Create(pt1.X+MM(2), pt1.Y+MM(2), pt1.Z+MM(2))
result=BlockBody.Create(pt1, pt2, ExtrudeType.Add)
b0=result.CreatedBody
for i in range(11):
mySel = Selection.Create(b0)
axis = Line.Create(Point.Origin, Direction.DirZ)
options = MoveOptions()
options.Copy = True
result = Move.Rotate(mySel, axis, (i+1)*DEG(30), options)
Selection.Clear()
ViewHelper.ZoomToEntity()
# Demo
from SpaceClaim.Api.V21 import Command
import os
ClearAll()
#Import the geometry
doc_path = os.path.dirname(GetActiveWindow().Document.Path)
DocumentInsert.Execute(os.path.join(doc_path, "valve1.dsco"))
Selection.Create(GetRootPart().Components[0]).SetActive()
c = Command.GetCommand("ImportComponentGroups")
c.Execute()
ViewHelper.ZoomToEntity()
#Fill the surface holes < criteria
criteria_radius = MM(7)
total_selection = Selection.Empty()
selection1 = PowerSelection.Faces.BySurfaceHoleRadius(criteria_radius,
PowerSelectOptions(True),
SearchCriteria.SizeComparison.SmallerOrEqual)
total_selection += selection1
total_selection.SetActive()
result = Fill.Execute(total_selection)
Remove all chamfers and rounds
criteria_radius = MM(2)
total_selection = PowerSelection.Faces.ByRoundRadius(criteria_radius,
PowerSelectOptions(True),
SearchCriteria.SizeComparison.SmallerOrEqual,
SearchCriteria.RoundType.All)
for body in GetRootPart().GetAllBodies():
for face in body.Faces:
if isinstance(face.Shape.Geometry, Cone):
total_selection += Selection.Create(face)
total_selection.SetActive()
result = Fill.Execute(total_selection)
#Create missing bodies from Named Selections and move them to new components
ComponentHelper.SetActive(Selection.Create(GetRootPart().Components[0]), None)
options = LoftOptions()
options.IsRuled = True
selection = Selection.CreateByGroups("inlet_1")
selection += Selection.CreateByGroups("inlet_2")
result = Loft.Create(selection, None, options)
selection = Selection.Create(result.CreatedBodies[0])
result = ComponentHelper.MoveBodiesToComponent(selection)
result.CreatedComponents[0].SetName("inlets")
#Simplify 1 body
body = GetActivePart().GetAllComponents("Valve")[0].GetBodies()[0]
zmax = 0
for face in body.Faces:
if face.EvalMid().Point.Z > zmax:
zmax = face.EvalMid().Point.Z
my_face = face
selection = Selection.Create(my_face) + Selection.Create(my_face.AdjacentFaces)
result = Fill.Execute(selection)
Remove / Translate / Copy Holes
sel = PowerSelection.Faces.BySurfaceHoleRadius(MM(3),
PowerSelectOptions(False, BodySelection.Create(GetRootPart().Bodies[0])),
SearchCriteria.SizeComparison.Equal)
secondarySelection = Selection.Empty()
options = FillOptions()
result = Fill.Execute(sel, secondarySelection, options, FillMode.ThreeD)
# Translate bigger hole Along X Handle
circ_face = PowerSelection.Faces.BySurfaceHoleRadius(MM(35),
PowerSelectOptions(False, BodySelection.Create(GetRootPart().Bodies[0])),
SearchCriteria.SizeComparison.Equal)
direction = Direction.Create(1, 0, 0)
options = MoveOptions()
result = Move.Translate(circ_face, direction, MM(45), options)
# Translate (copy) bigger hole Along X Handle
direction = Direction.Create(1, 0, 0)
options = MoveOptions()
options.CreatePatterns = True
options.Copy = True
result = Move.Translate(circ_face, direction, MM(-90), options)
Create Fluid Volume
part = GetRootPart()
body = part.Bodies[0]
ymin = 0
ymax = 0
zmax = 0
# access faces with openings (ymin, ymax, zmax)
for face in body.Faces:
if face.EvalMid().Point.Y < ymin:
ymin = face.EvalMid().Point.Y
ymin_face = face
if face.EvalMid().Point.Y > ymax:
ymax = face.EvalMid().Point.Y
ymax_face = face
if face.EvalMid().Point.Z > zmax:
zmax = face.EvalMid().Point.Z
zmax_face = face
options = VolumeExtractOptions()
selection = FaceSelection.Create(ymin_face, ymax_face, zmax_face)
#select seed face
secondarySelection = circ_face
result = VolumeExtract.Create(selection, secondarySelection, options)
External Connections such as MS-Excel
#Reference to Microsoft Excel
ClearAll()
clr.AddReference("Microsoft.Office.Interop.Excel")
import Microsoft.Office.Interop.Excel as Excel
import os
doc_path = os.path.dirname(GetActiveWindow().Document.Path)
doc_excel = Excel.ApplicationClass()
doc_excel.Visible = True
excel_file_name = "read_excel.xlsx"
wb = doc_excel.Workbooks.Open(os.path.join(doc_path,excel_file_name))
#or ws = workbook.Worksheets("Sheet1")
ws = wb.Worksheets[1]
#Read data from Excel file
i = 1
myX = ""
wloc = True
points = List[Point2D]()
while wloc:
myX = ws.Rows[i].Value2[0, 0]
if not isinstance(myX, str):
myY = ws.Rows[i].Value2[0, 1]
points.Add(Point2D.Create(MM(myX), MM(myY)))
i = i+1
if myX == "End":
wloc = False
wb.Close()
doc_excel.Quit()
#create spline curve from imported point data and create a surface body
ViewHelper.SetSketchPlane(Plane.PlaneXY)
result = SketchNurbs.CreateFrom2DPoints(True, points)
ViewHelper.SetViewMode(InteractionMode.Solid)
ViewHelper.ZoomToEntity()
Scripting in ANSYS DesignModeler
The script file is written in JScript (extension *.js). // Two slashes indicate a comment. Access to the DesignModeler application functions is accessible via the prefix 'agb.', as in the command: agb.Regen(); //Run 'Generate' command. Create a Boolean operation:var bool_addBodies= ag.gui .CreateBoolean();
bool_addBodies.Name = "Add Bodies";
bool_addBodies.Operation = 0;
ag.listview .ActivateItem("Tool Bodies");
agb.ClearSelections();
body_1 = ag.fm.Body(1);
agb.AddSelect(agc.TypeBody, body_1);
body_2 = ag.fm.Body(2);
agb.AddSelect(agc.TypeBody, body_2);
ag.listview .ItemValue = "Apply";
Script Constants: These must be prefixed with agc to be usable such as agc.Add //Add Material. FormNewPartFromAllBodies(); FormNewPartFromSelectedBodies(); Properties: 'Name' allows the part to be named; for example, px.Name = "Origin_x";
Scripting in Cadence's Fidelity Pointwise
The scripting language is known as Glyphs which is implemented as a set of Tcl/Tk (Tool command Language / Tool kit) procedures. Pointwise supports non-Tcl scripting (or binary code) applications through a feature called Glyph Server.Geometry Editing in FreeCAD
FreeCAD works using module or workbench defined in the drop-down shown below. Hover the mouse near the bottom right corner shown below to select the Navigation Style and associated mouse key mapping.
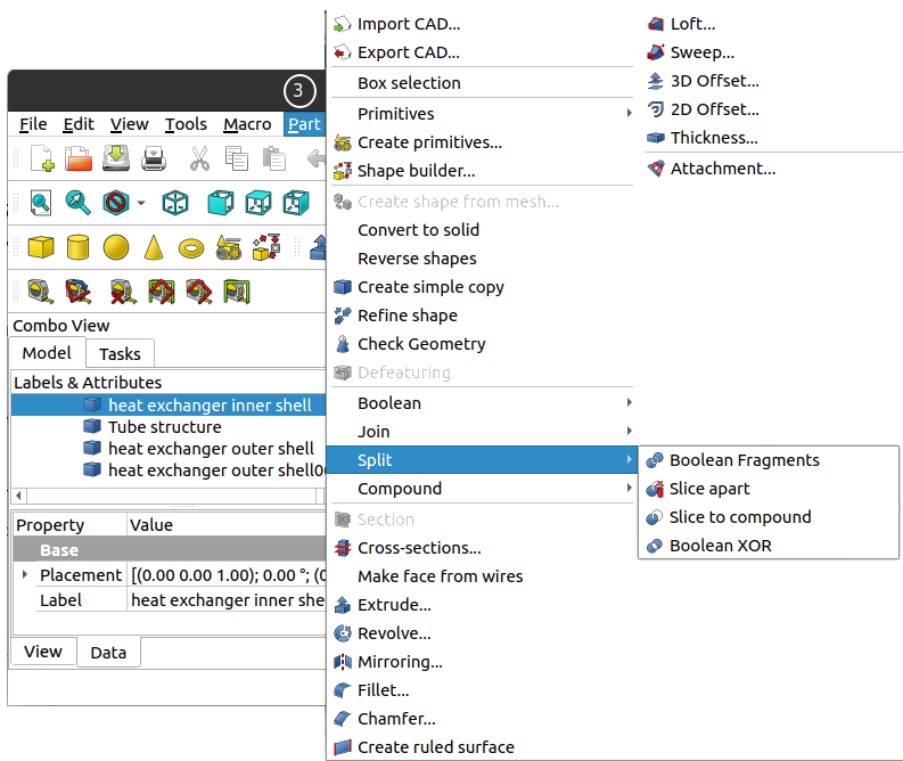
The content on CFDyna.com is being constantly refined and improvised with on-the-job experience, testing, and training. Examples might be simplified to improve insight into the physics and basic understanding. Linked pages, articles, references, and examples are constantly reviewed to reduce errors, but we cannot warrant full correctness of all content.
Template by OS Templates